题目内容
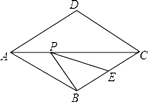
如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为________.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为________.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案