题目内容
20.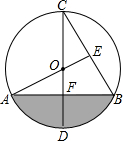 如图,已知CD为⊙O的直径,CD⊥AB,垂足为点F,∠C=30°,连结AO并延长交BC于点E.
如图,已知CD为⊙O的直径,CD⊥AB,垂足为点F,∠C=30°,连结AO并延长交BC于点E.(1)求证:AE⊥BC;
(2)若AO=1,求阴影部分的面积.
分析 (1)由垂径定理可知$\widehat{AD}$=$\widehat{BD}$,所以由圆周角定理可知:∠AOD=2∠C=60°,根据三角形内角和定理即可求出∠CEO=90°
(2)连接OB,分别求出扇形OAB,三角形OAB的面积即可求出阴影部分的面积.
解答 解:(1)∵CD⊥AB,
∴$\widehat{AD}$=$\widehat{BD}$,
∴由圆周角定理可知:∠AOD=2∠C,
∴∠COE=∠AOD=60°,
∴∠CEO=90°,
∴AE⊥BC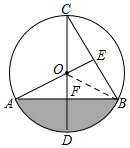
(2)连接OB,
由(1)可知:∠OAF=30°,
∴OF=$\frac{1}{2}$OA=$\frac{1}{2}$,
由勾股定理可知:AF=$\frac{\sqrt{3}}{2}$,
∴由垂径定理可知:AB=2AF=$\sqrt{3}$
∴△OAB的面积为:$\frac{1}{2}$AB•OF=$\frac{\sqrt{3}}{4}$
扇形OAB的面积为:$\frac{120°π×1}{360°}$=$\frac{π}{3}$
∴阴影部分的面积为:$\frac{π}{3}$-$\frac{\sqrt{3}}{4}$
点评 本题考查圆的综合问题,解题的关键是根据垂径定理求出∠AOB的度数,以及OF、AF的长度,本题属于基础题型.

练习册系列答案
相关题目
17.如图①是正方体的展开图,如果将其折成原来的正方体(如图②),那么与点M重合的两点应该是( )


| A. | S和Z | B. | W和Y | C. | U和Y | D. | T和V |
 如图,点D是CB延长线上一点,已知BE平分∠ABD,∠C=62°,∠ABD=124°,则BE∥AC吗?请说明理由.
如图,点D是CB延长线上一点,已知BE平分∠ABD,∠C=62°,∠ABD=124°,则BE∥AC吗?请说明理由.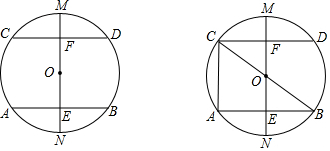
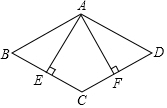 如图,在菱形ABCD中,E,F分别为BC,CD的中点,且AE⊥BC,AF⊥CD,垂足分别为E,F.求∠EAF的度数.
如图,在菱形ABCD中,E,F分别为BC,CD的中点,且AE⊥BC,AF⊥CD,垂足分别为E,F.求∠EAF的度数.