题目内容
1.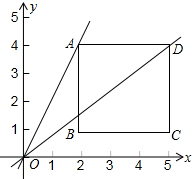 如图,在平面直角坐标系xOy中,正方形ABCD的顶点A在直线l:y=2x上,AB⊥x轴,顶点B的坐标为(2,1).
如图,在平面直角坐标系xOy中,正方形ABCD的顶点A在直线l:y=2x上,AB⊥x轴,顶点B的坐标为(2,1).(1)求正方形ABCD的面积;
(2)将直线l绕着点O按顺时方向旋转,当l经过顶点D时,直线l将正方形ABCD分成两个部分,试求这两个部分面积的比.
分析 (1)将x=2代入y=2x,可求得y=4,从而可求得AB=3,于是可求得正方形ABCD的面积;
(2)由正方形的边长为3可求得点D的坐标为(5,4),从而可求得直线OD的解析式,接下来求得OD与AB交点的坐标,从而可求得被分割的两部分的面积.
解答 解:(1)∵AB⊥x轴,
∴点A的横坐标为2.
将x=2代入得;y=2×2=4.
∴点A的坐标为(2,4).
∴AB=4-1=3.
∴正方形ABCD的面积=3×3=9.
(2)如图所示:记AB与OD的交点为E.
∵正方形的边长为3.
∴点D的坐标为(5,4).
设OD的解析式为y=kx,将(5,4)代入得:5k=4,
解得k=$\frac{4}{5}$.
∴直线OD的解析式为y=$\frac{4}{5}x$.
将x=2代入y=$\frac{4}{5}x$得:y=$\frac{8}{5}$.
∴AE=4-$\frac{8}{5}$=$\frac{12}{5}$,.
∴${S}_{△AED}=\frac{1}{2}×\frac{12}{5}×3$=$\frac{18}{5}$.
∴${S}_{EBCD}=9-\frac{18}{5}$=$\frac{27}{5}$.
∴S△AED:SEBCD=2:3.
点评 本题主要考查的是一次函数的图象和性质、正方形的性质、平行于坐标轴的直线上点的坐标特点,求得点A和点E的坐标是解题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
11.某小型木材厂对采购木材进行销售的获利情况,如下图所示:
该厂现采购木材140立方米,已知该厂每天能加工成品6立方米或半成品16立方米(两种加工不能同时进行,且每天只进行一种加工)
(1)该厂计划在10天内刚好加工完140立方米木材,则该厂加工成品和半成品各多少天?
(2)若该厂计划木材加工后再销售,且获利不能少于42200元,在该厂要加工这140立方米的木材需要多少天?
| 销售方式 | 直接销售 | 加工成半成品 | 加工成成品 |
| 每方米获利(元) | 100 | 250 | 450 |
(1)该厂计划在10天内刚好加工完140立方米木材,则该厂加工成品和半成品各多少天?
(2)若该厂计划木材加工后再销售,且获利不能少于42200元,在该厂要加工这140立方米的木材需要多少天?
9.甲队修路120m与乙队修路100m所用天数相同,已知甲队比乙队每天多修10m,设乙队每天修路xm.依题意,下面所列方程正确的是( )
| A. | $\frac{120}{x}=\frac{100}{x-10}$ | B. | $\frac{120}{x+10}=\frac{100}{x}$ | C. | $\frac{120}{x-10}=\frac{100}{x}$ | D. | $\frac{120}{x}=\frac{100}{x+10}$ |
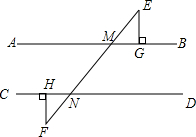 如图,直线EF和AB,CD分别相交于点M,N,EG⊥AB,FH⊥CD,垂足分别为G,H,且∠BME=53°,∠F=37°,试利用“三角形内角和等于180°”说明直线AB∥CD,EG∥FH.
如图,直线EF和AB,CD分别相交于点M,N,EG⊥AB,FH⊥CD,垂足分别为G,H,且∠BME=53°,∠F=37°,试利用“三角形内角和等于180°”说明直线AB∥CD,EG∥FH.