题目内容
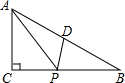如图，Rt△ABC，∠C=90°，∠B=30°，BC=6，D为AB中点，P为BC上一动点，连接AP、DP，则AP+DP的最小值是考点：轴对称-最短路线问题
专题：
分析：作A关于BC的对称点A'，连接A′B，易求∠A=60°，则PA=A'P，且△AA'B为等边三角形，AP+DP=A'P+PD为A'与直线AB之间的连接线段，其最小值为A'到AB的距离=BC=6，所以最小值为6．
解答：解：作A关于BC的对称点A'，连接A′B，
∵∠C=90°，∠B=30°，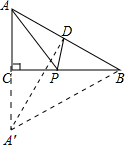
∴∠A=60°，
∵PA=A'P，
∴△AA'B为等边三角形，
∴AP+DP=A'P+PD为A'与直线AB之间的连接线段，
∴最小值为A'到AB的距离=BC=6，
故答案为：6．
∵∠C=90°，∠B=30°，
∴∠A=60°，
∵PA=A'P，
∴△AA'B为等边三角形，
∴AP+DP=A'P+PD为A'与直线AB之间的连接线段，
∴最小值为A'到AB的距离=BC=6，
故答案为：6．
点评：本题考查的是最短线路问题及等边三角形的性质，熟知两点之间线段最短的知识是解答此题的关键．
练习册系列答案
一线名师权威作业本系列答案
相关题目
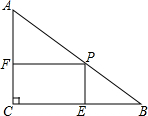如图，在Rt△ABC中，∠C=90°，∠B=30°，AB=12cm，点P是AB边上的一个动点，过点P作PE⊥BC于点E，PF⊥AC于点F，当PB=
如图，AC=DB，∠1=∠2，则△ABC≌△
如图，在△ABC中，已知AB=AC，D是BC边上的中点，∠B=30°，则∠DAC=