题目内容
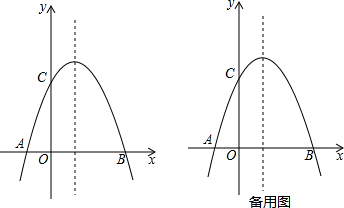
 已知抛物线y=x2-2ax+a2-2的顶点为A,P点在该抛物线的对称轴上,且在A点上方,PA=3.
已知抛物线y=x2-2ax+a2-2的顶点为A,P点在该抛物线的对称轴上,且在A点上方,PA=3.(1)求A、P点的坐标(用含a的代数式表示);
(2)点Q在抛物线上,求线段PQ的最小值;
(3)若直线y=x+a-2与该抛物线交于B、C两点,M点是线段BC的中点.当a的值在某范围内变化时,M点的运动轨迹是一条直线的一部分,请求出该直线的解析式,并写出自变量的取值范围.
考点:二次函数综合题
专题:
分析:(1)把抛物线的解析式化成顶点式,即可得出顶点坐标,根据已知即可求得P的坐标;
(2)设Q(m,(m-a)2-2),根据勾股定理即可求得PQ2=(m-a)2+[(m-a2)-3]2,令(m-a)2=n,得出PQ2=(n-
)2+
,即可求得PQ的最小值;
(3)联立方程,即可得到x2-(2a+1)x+a2-a=0,即可求得直线y=x+a-2与该抛物线交于B、C两点的横坐标、纵坐标的和,进而求得中点M的坐标,由M的坐标即可得出点M在直线y=2x-
上,根据△=(2a+1)2-4(a2-a)>0,即可求得的取值,进而求得
的取值,即直线y=2x-
的取值.
(2)设Q(m,(m-a)2-2),根据勾股定理即可求得PQ2=(m-a)2+[(m-a2)-3]2,令(m-a)2=n,得出PQ2=(n-
| 5 |
| 2 |
| 11 |
| 4 |
(3)联立方程,即可得到x2-(2a+1)x+a2-a=0,即可求得直线y=x+a-2与该抛物线交于B、C两点的横坐标、纵坐标的和,进而求得中点M的坐标,由M的坐标即可得出点M在直线y=2x-
| 5 |
| 2 |
| 2a+1 |
| 2 |
| 5 |
| 2 |
解答:解:(1)∵抛物线y=x2-2ax+a2-2,
∴y=(x-a)2-2,
∴A(a,-2),
∵P点在该抛物线的对称轴上,且在A点上方,PA=3.
∴P(a,1);
(2)∵点Q在抛物线y=x2-2ax+a2-2上,
∴设Q(m,(m-a)2-2),则PQ2=(m-a)2+[(m-a2)-3]2
令(m-a)2=n,则PQ2=n+(n-3)2=(n-
)2+
,
当n=
时,PQ2最小,即PQ最小
∴PQ的最小值=
=
;
(3)由
得x2-(2a+1)x+a2-a=0
∴x1+x2=2a+1
∴y1+y2=x1+x2+2a-4=4a-3,
∴M(
,
),
设M(x0,y0)
∴x0=
,y0=
,
∴y0=2x0-
,
∴点M在直线y=2x-
上
又∵△=(2a+1)2-4(a2-a)>0,则a>-
,
∴x0>
∴直线为y=2x-
(x>
).
∴y=(x-a)2-2,
∴A(a,-2),
∵P点在该抛物线的对称轴上,且在A点上方,PA=3.
∴P(a,1);
(2)∵点Q在抛物线y=x2-2ax+a2-2上,
∴设Q(m,(m-a)2-2),则PQ2=(m-a)2+[(m-a2)-3]2
令(m-a)2=n,则PQ2=n+(n-3)2=(n-
| 5 |
| 2 |
| 11 |
| 4 |
当n=
| 5 |
| 2 |
∴PQ的最小值=
|
| ||
| 2 |
(3)由
|
∴x1+x2=2a+1
∴y1+y2=x1+x2+2a-4=4a-3,
∴M(
| 2a+1 |
| 2 |
| 4a-3 |
| 2 |
设M(x0,y0)
∴x0=
| 2a+1 |
| 2 |
| 4a-3 |
| 2 |
∴y0=2x0-
| 5 |
| 2 |
∴点M在直线y=2x-
| 5 |
| 2 |
又∵△=(2a+1)2-4(a2-a)>0,则a>-
| 1 |
| 8 |
∴x0>
| 3 |
| 8 |
∴直线为y=2x-
| 5 |
| 2 |
| 3 |
| 8 |
点评:本题是二次函数的综合题,考查了抛物线的顶点和对称轴,求得线段的中点坐标是(3)的重点和关键.

练习册系列答案
相关题目
在-1.414,
,π,2+
,3.212212221…,3.14,
这些数中,无理数的个数为( )
| 2 |
| 3 |
| 1 |
| 7 |
| A、2 | B、3 | C、4 | D、5 |
截止2014年底,深圳市拥有各级公共图书馆743个,藏书总量约24910000册,用科学记数法表示我市藏书总量约为( )册.
| A、0.2491×108 |
| B、2.491×107 |
| C、2.491×108 |
| D、2491×104 |
 如图,抛物线y=x2-3x-18与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
如图,抛物线y=x2-3x-18与x轴交于A、B两点,与y轴交于点C,连接BC、AC.