题目内容
13．如图可以自由转动的转盘被3等分，指针落在每个扇形内的机会均等．
（1）现随机转动转盘一次，停止后，指针指向数字1的概率为$\frac{1}{3}$；
（2）小明和小华利用这个转盘做游戏，若采用下列游戏规则，你认为对双方公平吗？请用列表或画树状图的方法说明理由．
分析 （1）三个等可能的情况中出现1的情况有一种，求出概率即可；
（2）列表得出所有等可能的情况数，求出两人获胜的概率，比较即可得到结果．
解答 解：（1）根据题意得：随机转动转盘一次，停止后，指针指向1的概率为$\frac{1}{3}$；
故答案为：$\frac{1}{3}$；
（2）列表得：
| 1 | 2 | 3 | |
| 1 | （1，1） | （2，1） | （3，1） |
| 2 | （1，2） | （2，2） | （3，2） |
| 3 | （1，3） | （2，3） | （3，3） |
∴P（小明获胜）=$\frac{5}{9}$，P（小华获胜）=$\frac{4}{9}$，
∵$\frac{5}{9}$＞$\frac{4}{9}$，
∴该游戏不公平．
点评 此题考查了游戏公平性，以及列表法与树状图法，判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平．
练习册系列答案
相关题目
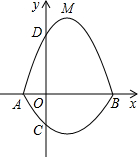如图，在平面直角坐标系xOy中，A、B为x轴上两点，C、D为y轴上的两点，经过点A、C、B的抛物线C1的一部分与经过点A、D、B的抛物线C2的一部分组合成一条封闭曲线，我们把这条封闭曲线叫做“蛋线”．已知点C的坐标为（0，-$\frac{3}{2}$），点M是抛物线C2：y=-x2+2x+3的顶点．