Question

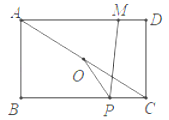
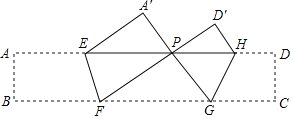
【题目】如图，把矩形ABCD沿EF，GH折叠，使点B，C落在AD上同一点P处，∠FPG＝90°，△A′EP的面积是8，△D′PH的面积是4，则矩形ABCD的面积等于_____．

Answer 1

【答案】8（3+2）

【解析】

由翻折可得∠A′＝∠FPG，所以得A′E∥PF，可以证明△AE′P∽△D′PH，根据相似三角形面积的比等于相似比的平方可求得A′E＝D′P，再根据△A′EP的面积是8可求A′P＝D′P＝4，从而AE＝A′E＝4，再根据勾股定理求得PE的长，进而求得D′H、PH，所以得AD＝AE+EP+PH+DH，最后求得矩形ABCD的面积．

解：由翻折可知：

∠A＝∠A′＝90°，∠D＝∠D′＝90°，

∵∠FPG＝90°，

∴∠A′＝∠FPG，

∴A′E∥PF，

∴∠A′EP＝∠D′PH，

∴△AE′P∽△D′PH，

∴，

∵AB＝CD，AB＝A′P，CD＝D′P，

∴A′P＝D′P，

∵，

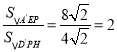∴A′E＝D′P，

∴S△A′EP＝A′EA′P＝×D′PD′P＝8，

解得D′P＝4（负值舍去），

∴A′P＝D′P＝4，

∴AE＝A′E＝4，

∴EP＝，

∴PH＝

DH＝D′H＝2，

∴AD＝AE+EP+PH+DH

＝4+4+2+2

＝6+4+2．

AB＝A′P＝4，

∴S矩形ABCD＝ABAD

＝4（6+4+2）

＝8（3+2+）．

故答案为：8（3+2）．