题目内容
(2004•玉溪)如图,AB是⊙O的直径,点D在AB的延长线上,且DC切⊙O于C点,∠CAD=30°,延长DC到点E,使∠CAE=∠CAD.(1)试探求AD与⊙O的半径有怎样的数量关系,并加以证明;
(2)求证:AC•CD=AE•OD.

【答案】分析:(1)要探求AD与⊙O半径的数量关系,因为AD=OD+⊙O的半径,即探求OD与⊙O半径的数量关系,为此连接OC,得直角△OCD,根据30°角所对的直角边等于斜边的一半求出答案;
(2)欲证AC•CD=AE•OD,即证AE:CD=AC:OD,可以通过证明△EAC∽△CDO求出.
解答: (1)解:AD是⊙O半径的3倍.
(1)解:AD是⊙O半径的3倍.
证明:连接OC,
∵DE是切线
∴OC⊥DE
∵OC=OA
∴∠CAO=∠OCA=30°
∴∠COD=∠CAO+∠OCA=60°
∴∠D=30°
∴OD=2OC
∴AD=3OC;
(2)证明:∵∠CAE=∠CAD=30°
∴∠EAD=60°=∠COD
∴OC∥AE
∴∠E=∠OCD=90°
又∠EAC=∠D=30°
∴△EAC∽△CDO
∴AE:CD=AC:OD
∴AC•CD=AE•OD.
点评:本题主要考查相似三角形的判定和切线的性质.
(2)欲证AC•CD=AE•OD,即证AE:CD=AC:OD,可以通过证明△EAC∽△CDO求出.
解答:
 (1)解:AD是⊙O半径的3倍.
(1)解:AD是⊙O半径的3倍.证明:连接OC,
∵DE是切线
∴OC⊥DE
∵OC=OA
∴∠CAO=∠OCA=30°
∴∠COD=∠CAO+∠OCA=60°
∴∠D=30°
∴OD=2OC
∴AD=3OC;
(2)证明:∵∠CAE=∠CAD=30°
∴∠EAD=60°=∠COD
∴OC∥AE
∴∠E=∠OCD=90°
又∠EAC=∠D=30°
∴△EAC∽△CDO
∴AE:CD=AC:OD
∴AC•CD=AE•OD.
点评:本题主要考查相似三角形的判定和切线的性质.

练习册系列答案
相关题目
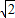 ≈1.414,
≈1.414,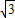 ≈1.732,结果保留整数)
≈1.732,结果保留整数)