题目内容
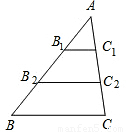
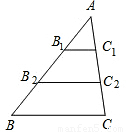
（2004•玉溪）如图，在⊙O中，∠AOB=130°，∠ABC=40°，则∠D= 度．
【答案】分析：解答此题的关键是连接AD，构造出圆周角，再利用圆周角定理解答，即∠ADB=
∠AOB=
×130°=65°，
∠1=∠ABC=40°，即可求∠D的度数．
解答：
解：连接AD，
∵∠AOB=130°，
∴∠ADB=
∠AOB=
×130°=65°，
∵∠1=∠ABC=40°，
∴∠BDC=∠2=∠ADB-∠1=65°-40°=25°．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
∠AOB=×130°=65°，∠1=∠ABC=40°，即可求∠D的度数．
解答：
解：连接AD，∵∠AOB=130°，
∴∠ADB=
∠AOB=×130°=65°，∵∠1=∠ABC=40°，
∴∠BDC=∠2=∠ADB-∠1=65°-40°=25°．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
相关题目
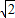≈1.414，
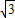≈1.732，结果保留整数）
