题目内容
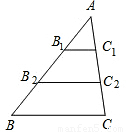
（2004•玉溪）如图，△ABC中，BC=4，B1、C1分别是AB、AC的中点，B2、C2分别是B1B、C1C中点，则B2C2的长是 ．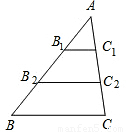
【答案】分析：首先根据三角形的中位线定理，得到B1C1和BC的数量关系与位置关系，再根据梯形的中位线定理求得B2C2的长．
解答：解：由题意，得B1C1为△ABC的中位线，
∴B1C1=
BC=2，B1C1∥BC．
∵B2、C2分别是B1B、C1C中点，
∴B2C2=
（BC+B1C1）=3．
点评：本题用到的知识点为：三角形的中位线等于三角形第三边的一半，梯形中位线=
（上底+下底）．
解答：解：由题意，得B1C1为△ABC的中位线，
∴B1C1=
BC=2，B1C1∥BC．∵B2、C2分别是B1B、C1C中点，
∴B2C2=
（BC+B1C1）=3．点评：本题用到的知识点为：三角形的中位线等于三角形第三边的一半，梯形中位线=
（上底+下底）． 
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
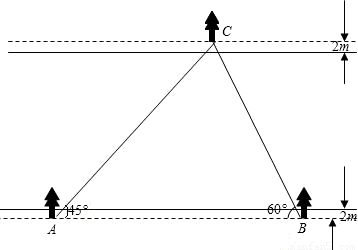
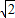≈1.414，
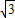≈1.732，结果保留整数）
