题目内容
4.按数字排列规律:$\frac{1}{2},\frac{4}{3},\frac{9}{4},\frac{16}{5},\frac{25}{6}$…,写出第n个数为$\frac{{n}^{2}}{n+1}$(n为正整数).分析 观察已知数字排列,发现,分数分母依次增加1,分子为自然数的平方,结合分子分母和序号的关系得出答案.
解答 解:按数字排列规律:
第1个数:$\frac{1}{2}$=$\frac{{1}^{2}}{1+1}$,
第2个数:$\frac{4}{3}$=$\frac{{2}^{2}}{2+1}$,
第3个数:$\frac{9}{4}$=$\frac{{3}^{2}}{3+1}$,
…,
第n个数:$\frac{n^2}{n+1}$.
故答案为:$\frac{n^2}{n+1}$.
点评 题目考查了数字的变化规律,通过数字与序号之间的规律考查学生观察能力和总结能力,题目整体较为简单,适合随堂训练.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
13.若△ABC∽△A′B′C′,相似比为2:3,则△ABC与△A′B′C′的周长的比为( )
| A. | 2:3 | B. | 4:9 | C. | 3:2 | D. | $\sqrt{2}$:$\sqrt{3}$ |
14.下列说法正确的是( )
| A. | “任意画一个等边三角形,它是轴对称图形”是随机事件 | |
| B. | “任意画一个平行四边形,它是中心对称图形”是必然事件 | |
| C. | “概率为0.000001的事件”是不可能事件 | |
| D. | 任意掷一枚质地均匀的硬币10次,正面朝上的次数一定是5 |

 已知在平面直角坐标系xOy中,抛物线y=$\frac{1}{2}$x2+bx+c经过点A(4,0)、点C(0,-4),点B与点A关于这条抛物线的对称轴对称.
已知在平面直角坐标系xOy中,抛物线y=$\frac{1}{2}$x2+bx+c经过点A(4,0)、点C(0,-4),点B与点A关于这条抛物线的对称轴对称.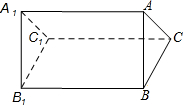 如图是一个三棱柱的图形,它共有五个面,其中三个面是长方形,两个面是三角形,请写出符合下列条件的棱(说明:每个空只需写出一条即可).
如图是一个三棱柱的图形,它共有五个面,其中三个面是长方形,两个面是三角形,请写出符合下列条件的棱(说明:每个空只需写出一条即可).