题目内容
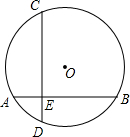 如图,在⊙O中,AB⊥CD于E,当AE=2cm,EB=6cm,ED=3cm,EC=4cm,求:
如图,在⊙O中,AB⊥CD于E,当AE=2cm,EB=6cm,ED=3cm,EC=4cm,求:(1)OE的长;
(2)⊙O的半径长.
考点:垂径定理,勾股定理
专题:计算题
分析:(1)过O作OF⊥CD,OG⊥AB,连接OE,OB,利用垂径定理得到F,G分别为CD,AB的中点,由CE-CF求出EF的长,即为OG的长,由EB-GB求出EG的长,在直角三角形OEG中,利用勾股定理求出OE的长即可;
(2)在直角三角形OGB中,利用勾股定理求出OB的长,即为圆的半径长.
(2)在直角三角形OGB中,利用勾股定理求出OB的长,即为圆的半径长.
解答: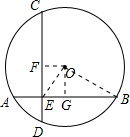 解:(1)过O作OF⊥CD,OG⊥AB,连接OE,OB,
解:(1)过O作OF⊥CD,OG⊥AB,连接OE,OB,
由垂径定理得到F为CD中点,G为AB中点,
∴CF=DF=
CD=
(CE+ED)=3.5cm,AG=BG=
AB=
(AE+EB)=4cm,
∴OF=EG=AG-AE=2cm,OG=FE=CE-CF=0.5cm,
在Rt△OEG中,利用勾股定理得:OE=
=
cm;
(2)在Rt△OGB中,OG=0.5cm,BG=4cm,
根据勾股定理得:OB=
=
cm.
 解:(1)过O作OF⊥CD,OG⊥AB,连接OE,OB,
解:(1)过O作OF⊥CD,OG⊥AB,连接OE,OB,由垂径定理得到F为CD中点,G为AB中点,
∴CF=DF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴OF=EG=AG-AE=2cm,OG=FE=CE-CF=0.5cm,
在Rt△OEG中,利用勾股定理得:OE=
| 22+0.52 |
| ||
| 2 |
(2)在Rt△OGB中,OG=0.5cm,BG=4cm,
根据勾股定理得:OB=
| 42+0.52 |
| ||
| 2 |
点评:此题考查了垂径定理,勾股定理,以及矩形的性质,熟练掌握垂径定理是解本题的关键.

练习册系列答案
相关题目
在Rt△ABC中,如果各边长度都扩大3倍,那么锐角A的各个三角函数值( )
A、都缩小
| ||
| B、都不变 | ||
| C、都扩大3倍 | ||
| D、无法确定 |