题目内容
8.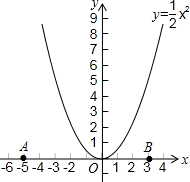 如图,A(-5,0),B(3,0),抛物线如图所示.
如图,A(-5,0),B(3,0),抛物线如图所示.(1)在抛物线上是否存在点C,D.使四边形ABCD为平行四边形?若存在,求出C,D的坐标;若不存在,说明理由.
(2)在(1)的条件下,在抛物线的对称轴上找到一点P,使△ADP的周长最小,求出点P的坐标.
(3)在(1)的条件下,在直线0C上是否存在点Q,使三角形CDQ是等腰三角形?若存在,直接写出点Q的坐标;若不存在,说明理由.
分析 (1)根据平行四边形的性质,可得CD与AB的关系,根据C与D关于y轴对称,可得答案;
(2)根据线段垂直平分线的性质,线段的性质,可得AC与y轴的交点,根据自变量与函数值的对应关系,可得答案;
(3)分类讨论:当DQ=CQ时,当DC=CQ时,当DC=DQ,根据勾股定理,可得关于m的方程,根据解方程,可得答案.
解答 解:(1)四边形ABCD为平行四边形,得
CD∥AB,CD=AB=8.
C、D关于对称轴y轴对称,得
C横坐标为4,D的横坐标为-4,
当x=4时,y=$\frac{1}{2}$×42=8,即C(4,8);
当x=-4时,y=$\frac{1}{2}$×(-4)2=8,即D(-4,8);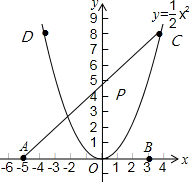 (2)如图,连接AC交y轴于P点,AD+AP+PD=AC+AD,
(2)如图,连接AC交y轴于P点,AD+AP+PD=AC+AD,
设AC的解析式为y=kx+b,
将A、C点坐标代入,得
$\left\{\begin{array}{l}{-5k+b=0}\\{4k+b=8}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{8}{9}}\\{b=\frac{40}{9}}\end{array}\right.$,
直线AC的解析式为y=$\frac{8}{9}$x+$\frac{40}{9}$,
当x=0时,y=$\frac{40}{9}$,
即P(0,$\frac{40}{9}$);
(3)OC的解析式为y=2x,设Q(m,2m),
①当DQ=CQ时,(m+4)2+(2m-8)2=(m-4)2+(2m-8)2,解得m=0,即Q1(0,0);
②当DC=CQ时,(m-4)2+(2m-8)2=82,化简,的5m2-40m+16=0,解得m=4±$\frac{8\sqrt{5}}{5}$,
当m=4+$\frac{8\sqrt{5}}{5}$时,y=2m=8+$\frac{16\sqrt{5}}{5}$,Q2(4+$\frac{8\sqrt{5}}{5}$,8+$\frac{16\sqrt{5}}{5}$);
当m=4-$\frac{8\sqrt{5}}{5}$时,y=8-$\frac{16\sqrt{5}}{5}$,Q3(4-$\frac{8\sqrt{5}}{5}$,8-$\frac{16\sqrt{5}}{5}$);
③当DC=DQ时,(m+4)2+(2m-8)2=82,化简,得5m2-24m+16=0,解得m=4,m=$\frac{4}{5}$,
当m=4时,y=2m=8,Q4(4,8),
当m=$\frac{4}{5}$时,y=2m=$\frac{8}{5}$,Q5($\frac{4}{5}$,$\frac{8}{5}$),
综上所述:Q1(0,0);
Q2(4+$\frac{8\sqrt{5}}{5}$,8+$\frac{16\sqrt{5}}{5}$);Q3(4-$\frac{8\sqrt{5}}{5}$,8-$\frac{16\sqrt{5}}{5}$);Q4(4,8),Q5($\frac{4}{5}$,$\frac{8}{5}$).
点评 本题考查了二次函数综合题,利用了平行四边形的性质得出DC与AB的关系是解题关键;利用了线段垂直平分线的性质,线段的性质;利用勾股定理的出关于m的方程是解题关键,要分类讨论,以防遗漏.

 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案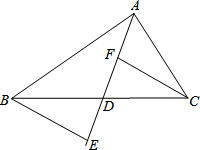 如图,在△ABC中,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.请你添加一个条件,使△BDE≌△CDF (不再添加其它线段,不再标注或使用其他字母),并给出证明.
如图,在△ABC中,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.请你添加一个条件,使△BDE≌△CDF (不再添加其它线段,不再标注或使用其他字母),并给出证明. 如图,等边△ABC中,D是AB边上的动点,以CD为一边向上作等边△EDC,连接AE.(1)求证:AE∥BC.
如图,等边△ABC中,D是AB边上的动点,以CD为一边向上作等边△EDC,连接AE.(1)求证:AE∥BC.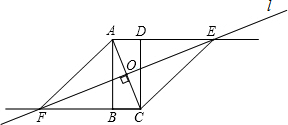 如图,四边形ABCD是矩形,直线l垂直平分线段AC,垂足为O,直线l分别与线段AD、CB的延长线交于点E、F.试判定四边形AFCE的形状,并说明理由.
如图,四边形ABCD是矩形,直线l垂直平分线段AC,垂足为O,直线l分别与线段AD、CB的延长线交于点E、F.试判定四边形AFCE的形状,并说明理由.