题目内容
8.已知x2-3x+1=0,求$\sqrt{{x}^{2}+\frac{1}{x^2}-2}$的值.分析 把已知等式两边除以x得到x+$\frac{1}{x}$=3,再利用完全平方公式变形得到原式=$\sqrt{(x+\frac{1}{x})^{2}-4}$,然后利用整体代入的方法计算.
解答 解:∵x2-3x+1=0,
∴x-3+$\frac{1}{x}$=0,即x+$\frac{1}{x}$=3,
∴原式=$\sqrt{(x+\frac{1}{x})^{2}-4}$
=$\sqrt{{3}^{2}-4}$
=$\sqrt{5}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.也考查了代数式的变形能力.

练习册系列答案
相关题目
13.2017年某市中考体育考试包括必考和选考两项.必考项目:男生1000米跑;女生800米跑;选考项目(五项中任选两项):A.掷实心球、B.篮球运球、C.足球运球、D.立定跳远、E.一分钟跳绳.那么小丽同学考“800米跑、立定跳远、一分钟跳绳”的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{10}$ |
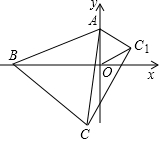 如图,在平面直角坐标系中,点A的坐标是(0,2),点B从坐标原点O出发,沿x轴负半轴运动,以AB为边作等边三角形ABC(A,B,C按逆时针顺序排列),当点B在原点O时,记此时的等边三角形为△AOC1.
如图,在平面直角坐标系中,点A的坐标是(0,2),点B从坐标原点O出发,沿x轴负半轴运动,以AB为边作等边三角形ABC(A,B,C按逆时针顺序排列),当点B在原点O时,记此时的等边三角形为△AOC1.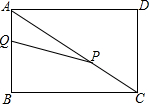 如图,在矩形ABCD中.AB=3cm.Bc=4cm.动点P以2cm/秒的速度从点C出发,沿CA向点A移动.同时动点Q以1cm/秒的速度从点A出发沿AB向点B移动.设P、Q两点移动t秒.
如图,在矩形ABCD中.AB=3cm.Bc=4cm.动点P以2cm/秒的速度从点C出发,沿CA向点A移动.同时动点Q以1cm/秒的速度从点A出发沿AB向点B移动.设P、Q两点移动t秒. 如图,已知?ABCD和?EBFD,求证:AE=CF.
如图,已知?ABCD和?EBFD,求证:AE=CF.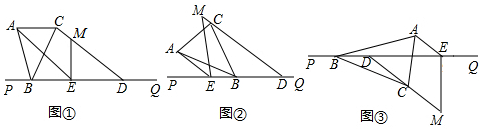

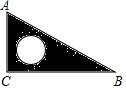 如图,一个直角三角形ABC的直角边BC=a,AC=b,三角形内部圆的半径为r.
如图,一个直角三角形ABC的直角边BC=a,AC=b,三角形内部圆的半径为r.