题目内容
如图,∆ABC中,D为AB的中点,E为AC上一点,过D作DF∥BE交AC于O,EF∥AB。

(1)猜想:OD与OF之间的关系是 。
(2)证明你的猜想。
【答案】
解:(1)OD=OF
(2)∵DF∥BE,EF∥AB
∴四边形DBEF是平行四边形
∴BD=EF
又∵AD=BD
∴AD=EF
又EF∥AB
∴∠DAO=∠FEO
又∠AOD=∠EOF
∴把∆FEO绕点O旋转1800后可与∆DAO重合
∴∆FEO≌∆DAO
∴OF=OD
【解析】(1)0D=OF,
(2)由已知可得四边形BDFE是平行四边形,从而可得BD=EF,由中点的定义可得AD=BD,再根据平行线的性质即可得到∠ADO=∠EFO,∠DAO=∠FEO,从而可利用ASA判定△ADO≌△EFO,根据全等三角形的对应边相等即可得到OD=OF,OA=OE,即得到AE与DF互相平分,或连接AF、DE,然后证明四边形DEFA是平行四边形,再根据平行四边形的对角线互相平分证明.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目


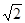 ,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n
,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n
 ;
;