Question

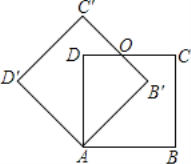
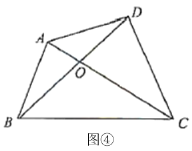
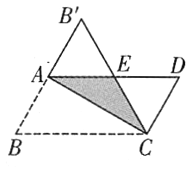
【题目】如图，在平行四边形纸片中，，将纸片沿对角线对折，边与边交于点，此时恰为等边三角形，则重叠部分的面积为_________．

Answer 1

【答案】

【解析】

首先根据等边三角形的性质可得A B'=AE=E B'，∠B'=∠B'EA=60°，根据折叠的性质，∠BCA=∠B'CA，，再证明∠B'AC=90°，再证得S△AEC=S△AEB'，再求S△A B'C进而可得答案．

解：∵为等边三角形，

∴A B'=AE=E B'，∠B'=∠B'EA=60°，
根据折叠的性质，∠BCA=∠B'CA，
∵四边形ABCD是平行四边形，
∴AD//BC，AD=BC，AB=CD，
∴∠B'EA=∠B'CB，∠EAC=∠BCA，
∴∠ECA=∠BCA=30°,

∴∠EAC=30°，
∴∠B'AC=90°，
∵,
∴B'C=8,

∴AC==,
∵B'E=AE=EC,

∴S△AEC=S△AEB'= S△A B'C= × ×4×=,

故答案为.