Question

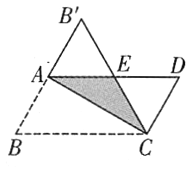
【题目】如图，AB 为⊙O 的直径，点 C 为⊙O 上一点，AD 和过点 C 的切线相互垂直，垂足为 D．

(1)求证：AC 平分∠DAB；

(2)AD 交⊙O 于点 E，若 AD＝3CD＝9，求 AE 的长度．

Answer 1

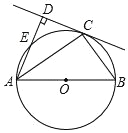
【答案】(1)见解析：（2）8.

【解析】

(1) 连接OC,根据AB为⊙0的直径, CD为⊙0的的切线可得AD//OC, 根据两直线平行, 内错角相等可得∠CAD＝∠ACO,即可由∠OAC＝∠ACO得到∠CAD＝∠OAC, 即可得证AC平分∠DAB.

(2) 连接CE, 易证得△CDE∽△ADC，可得＝，即 ＝， 解得，DE＝1，可得AE的长.

证明：（1）连接 OC，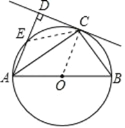

∵CD 是⊙ O 的切线，

∴OC⊥CD，又 AD⊥CD，

∴AD∥CO，

∴∠CAD＝∠ACO，

∵OA＝OC，

∴∠OAC＝∠ACO，

∴∠CAD＝∠OAC，即 AC 平分∠DAB；

（2）连接 EC，

由弦切角定理得，∠CAD＝∠ECD，又∠ADC＝∠CDE＝90°，

∴△CDE∽△ADC，

∴＝，即 ＝， 解得，DE＝1，

∴AE＝8．