题目内容
 已知,如图,在Rt△ABC中,∠C=90°,点E在AC上,AB=
已知,如图,在Rt△ABC中,∠C=90°,点E在AC上,AB=| 1 |
| 2 |
求证:∠CBA=3∠CBE.
考点:直角三角形斜边上的中线,等腰三角形的判定与性质
专题:证明题
分析:取DE的中点F,连接AF,根据直角三角形的性质求出AF=DF=FE=
DE,推出DF=AF=AB,根据等腰三角形的性质求出∠D=∠DAF,∠AFB=∠ABF,求出∠ABF=2∠D,∠CBE=∠D,即可得出答案.
| 1 |
| 2 |
解答:证明:
取DE的中点F,连接AF,
∵AD∥BC,∠ACB=90°,
∴∠DAE=∠ACB=90°,
∴AF=DF=EF=
DE,
∵AB=
DE,
∴DF=AF=AB,
∴∠D=∠DAF,∠AFB=∠ABF,
∴∠AFB=∠D+∠DAF=2∠D,
∴∠ABF=2∠D,
∵AD∥BC,
∴∠CBE=∠D,
∴∠CBA=∠CBE+∠ABF=3∠CBE.

取DE的中点F,连接AF,
∵AD∥BC,∠ACB=90°,
∴∠DAE=∠ACB=90°,
∴AF=DF=EF=
| 1 |
| 2 |
∵AB=
| 1 |
| 2 |
∴DF=AF=AB,
∴∠D=∠DAF,∠AFB=∠ABF,
∴∠AFB=∠D+∠DAF=2∠D,
∴∠ABF=2∠D,
∵AD∥BC,
∴∠CBE=∠D,
∴∠CBA=∠CBE+∠ABF=3∠CBE.
点评:本题考查了等腰三角形的性质,直角三角形的性质,平行线的性质,三角形的外角性质的应用,能正确作出辅助线是解此题的关键,难度适中.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
若等腰三角形的一个外角为100°,则它的底角为( )
| A、30°或50° |
| B、50° |
| C、50°或80° |
| D、80° |
某项工程由甲队单独做需18天完成,由乙队单独做只需甲队的一半时间完成.设两队合作需x天完成,则可得方程( )
A、
| ||||
B、(
| ||||
C、
| ||||
D、(
|
如果单项式-
xay2与
ybx3是同类项,那么a+b的值为( )
| 1 |
| 2 |
| 1 |
| 3 |
| A、-1 | B、4 | C、5 | D、6 |
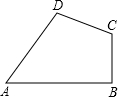 如图,在四边形ABCD中,AB=AD=6cm,CB=CD=8cm,且∠B=90°,该四边形存在内切吗?如果存在,请计算内切圆的半径.
如图,在四边形ABCD中,AB=AD=6cm,CB=CD=8cm,且∠B=90°,该四边形存在内切吗?如果存在,请计算内切圆的半径.