Question

2．如图，在平面直角坐标系中，已知点A（-1，0），B（3，2），将线段AB绕点A旋转90°，得到线段AB′，则点B′的坐标是（-3，4）或（1，-4）．

Answer 1

分析 由于题目没有说明顺时针旋转还是逆时针旋转，故需要分情况讨论．

解答 解：当AB绕点A逆时针旋转90°，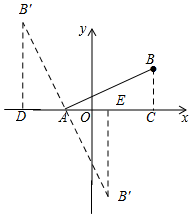
此时过点B′作B′D⊥x轴于点D，
∵∠BAC+∠B′AD=90°，
∠DB′A+∠B′AD=90°，
在△B′DA与△ACB中，
$\left\{\begin{array}{l}{∠B′DA=∠ACB}\\{∠DB′A=∠BAC}\\{AB′=AB}\end{array}\right.$
∴△B′DA≌△ACB（AAS），
∴AD=BC，B′D=AC
∵A（-1，0），B（3，2），
∴BC=2，AC=4，
∴B′（-3，4），
当AB绕点A顺时针旋转90°时，
过点B′作B′E⊥x轴于点E，
同理可求得：B′（1，-4）
故答案为：（-3，4）或（1，-4）

点评 本题考查考查旋转的性质，涉及旋转的三要素，全等三角形的性质与判定．