题目内容
3.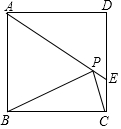 如图,在正方形ABCD中,AD=2$\sqrt{3}$,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为9-5$\sqrt{3}$.
如图,在正方形ABCD中,AD=2$\sqrt{3}$,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为9-5$\sqrt{3}$.
分析 根据旋转的想知道的PB=BC=AB,∠PBC=30°,推出△ABP是等边三角形,得到∠BAP=60°,AP=AB=2$\sqrt{3}$,解直角三角形得到CE=2$\sqrt{3}$-2,PE=4-2$\sqrt{3}$,过P作PF⊥CD于F,于是得到结论.
解答 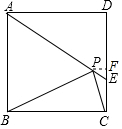 解:∵四边形ABCD是正方形,
解:∵四边形ABCD是正方形,
∴∠ABC=90°,
∵把边BC绕点B逆时针旋转30°得到线段BP,
∴PB=BC=AB,∠PBC=30°,
∴∠ABP=60°,
∴△ABP是等边三角形,
∴∠BAP=60°,AP=AB=2$\sqrt{3}$,
∵AD=2$\sqrt{3}$,
∴AE=4,DE=2,
∴CE=2$\sqrt{3}$-2,PE=4-2$\sqrt{3}$,
过P作PF⊥CD于F,
∴PF=$\frac{\sqrt{3}}{2}$PE=2$\sqrt{3}$-3,
∴三角形PCE的面积=$\frac{1}{2}$CE•PF=$\frac{1}{2}$×(2$\sqrt{3}$-2)×(2$\sqrt{3}$-3)=9-5$\sqrt{3}$,
故答案为:9-5$\sqrt{3}$.
点评 本题考查了旋转的性质,正方形的性质,等边三角形的判定和性质,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
13.《九章算术》“方程”篇中有这样一道题“今有甲乙二人持钱不知其数,甲得乙半面钱五十,乙得甲太半(注:太半,意思为三分之二)而钱亦五十.问甲、乙持钱各几何?”若设甲、乙原各持钱x,y,则根据题意可列方程组( )
| A. | $\left\{\begin{array}{l}{x+\frac{1}{2}y=50}\\{y+\frac{2}{3}x=50}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-\frac{1}{2}y=50}\\{y-\frac{2}{3}x=50}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+\frac{1}{2}x=50}\\{y+\frac{2}{3}y=50}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y+\frac{1}{2}x=50}\\{x+\frac{2}{3}y=50}\end{array}\right.$ |
14.如果a>b,那么下列结论一定正确的是( )
| A. | a-3<b-3 | B. | 3-a<3-b | C. | ac>bc | D. | a2>b2 |
11.sin60°的值为( )
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
18. 如图是一个正方体的表面展开图,则原正方体中与“美”字所在面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“美”字所在面相对的面上标的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“美”字所在面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“美”字所在面相对的面上标的字是( )| A. | 丽 | B. | 张 | C. | 家 | D. | 界 |
8. 五星红旗上的每一个五角星( )
五星红旗上的每一个五角星( )
 五星红旗上的每一个五角星( )
五星红旗上的每一个五角星( )| A. | 是轴对称图形,但不是中心对称图形 | |
| B. | 是中心对称图形,但不是轴对称图形 | |
| C. | 既是轴对称图形,又是中心对称图形 | |
| D. | 既不是轴对称图形,也不是中心对称图形 |
20.下列每一组数据中的三个数值分别为三角形三边的长,其中不能构成直角三角形的是( )
| A. | 9,12,15 | B. | 7,24,25 | C. | $\sqrt{3}$,2,$\sqrt{5}$ | D. | 9,40,41 |