题目内容
20.下列每一组数据中的三个数值分别为三角形三边的长,其中不能构成直角三角形的是( )| A. | 9,12,15 | B. | 7,24,25 | C. | $\sqrt{3}$,2,$\sqrt{5}$ | D. | 9,40,41 |
分析 欲判断是否为勾股数,必须根据勾股数是正整数,同时还需验证两小边的平方和是否等于最长边的平方.
解答 解:A、92+122=152,能够成三角形,不符合题意;
B、72+242=252,能构成直角三角形,不符合题意;
C、($\sqrt{3}$)2+22≠($\sqrt{5}$)2,不能构成直角三角形,符合题意;
D、92+402=412,能构成直角三角形,不符合题意.
故选C.
点评 此题主要考查了勾股定理的逆定理:已知△ABC的三边满足a2+b2=c2,则△ABC是直角三角形.

练习册系列答案
相关题目
11.下列计算正确的是( )
| A. | (a3)2=a6 | B. | a2+a4=2a2 | C. | a3a2=a6 | D. | (3a)2=a6 |
15.随着网络购物的兴起,截止到2017年3月深圳市物流产业增加值达到176.6亿元,若把数176.6亿用科学记数法表示是( )
| A. | 1.766×108 | B. | 1.766×1010 | C. | 1.766×109 | D. | 0.1766×1011 |
5.计算a3×(-a)5的结果是( )
| A. | a8 | B. | -a8 | C. | a15 | D. | -a15 |
9.关于x,y的方程组$\left\{\begin{array}{l}{x+ky=2}\\{x+y=3}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=△}\end{array}\right.$,其中y的值被盖住了,不过小红仍求出了k,则k的值是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
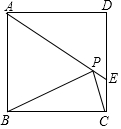 如图,在正方形ABCD中,AD=2$\sqrt{3}$,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为9-5$\sqrt{3}$.
如图,在正方形ABCD中,AD=2$\sqrt{3}$,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为9-5$\sqrt{3}$.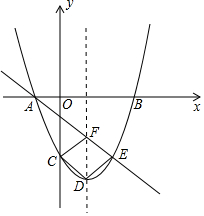 如图,二次函数y=ax2+bx+c的图象与x轴相交于点A(-1,0)与B,与y轴相交于点C(0,-3),抛物线的对称轴为直线x=1.
如图,二次函数y=ax2+bx+c的图象与x轴相交于点A(-1,0)与B,与y轴相交于点C(0,-3),抛物线的对称轴为直线x=1. 如图,将矩形ABCD沿对角线BD对折,点C落在E处,BE与AD相交于点F.
如图,将矩形ABCD沿对角线BD对折,点C落在E处,BE与AD相交于点F.