题目内容
(1)(a-2)2-6(2-a),其中a=-2.
(2)(
)2-(
)2,其中a=-
,b=2.
(2)(
| a+b |
| 2 |
| a-b |
| 2 |
| 1 |
| 8 |
分析:(1)将原式提取公因式后代入已知数即可求解;
(2)利用平方差公式展开后代入计算即可.
(2)利用平方差公式展开后代入计算即可.
解答:解:(1)(a-2)2-6(2-a)
=(a-2)(a+4),
∵a=-2,
∴原式=(-2-2)×(-2+4)=-4×2=-8.
(2)(
)2-(
)2
=
×
=ab,
∵a=-
,b=2.
∴原式=-
×2=-
;
=(a-2)(a+4),
∵a=-2,
∴原式=(-2-2)×(-2+4)=-4×2=-8.
(2)(
| a+b |
| 2 |
| a-b |
| 2 |
=
| a+b+a-b |
| 2 |
| a+b-a+b |
| 2 |
=ab,
∵a=-
| 1 |
| 8 |
∴原式=-
| 1 |
| 8 |
| 1 |
| 4 |
点评:本题考查了因式分解的应用,解题的关键是将原式进行正确的因式分解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
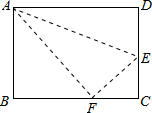 如图,长方形ABCD中,已知AB=8cm,BC=10cm,将AD沿直线AF折叠,使得点D落在BC边上的点E处,则CF=
如图,长方形ABCD中,已知AB=8cm,BC=10cm,将AD沿直线AF折叠,使得点D落在BC边上的点E处,则CF=