题目内容
18.综合与实践问题情境:
两张矩形纸片ABCD和CEFC完全相同,且AB=CE,AD>AB.
操作发现:
(1)如图1,点D在GC上,连接AC,CF,GE,AG,则AC和CF有何数量关系和位置关系?并说明理由.
实践探究:
(2)如图2,将图1中的纸片CEFG以点C为旋转中心逆时针旋转,当点D落在GE上时停止旋转,则AG和GF在同一直线上吗?请判断,并说明理由.

分析 (1)由矩形的性质得出∠ADC=∠GCE=∠CGF=90°,AC=CF,CD=CE,△ADC≌△CGF≌△GCE,得出AC=GE,∠DAC=∠GCF,∠ACD=∠GEC,由角的互余关系得出∠ACD+∠GCF=90°,即可得出结论;
(2)由旋转的性质得:CD=CE,由等腰三角形的性质得出∠CDE=∠CED,证出∠ACD=∠CDE,得出AC∥GE,证出四边形ACEG是平行四边形,得出AG∥CE,由平行线的性质得出∠AGC=∠GCE=90°,证出∠AGC+∠CGF=180°,即可得出结论.
解答 解:(1)AC=CF,AC⊥CF;理由如下:
∵四边形ABCD和四边形CEFC是矩形,且完全相同,AB=CE,
∴∠ADC=∠GCE=∠CGF=90°,AC=CF,CD=CE,△ADC≌△CGF≌△GCE,
∴AC=GE,∠DAC=∠GCF,∠ACD=∠GEC,
∵∠DAC+∠ACD=90°,
∴∠ACD+∠GCF=90°,
即∠ACF=90°,
∴AC⊥CF;
(2)AG和GF在同一直线上;理由如下:
由旋转的性质得:CD=CE,
∴∠CDE=∠CED,
∵∠ACD=∠GEC,
∴∠ACD=∠CDE,
∴AC∥GE,
又∵AC=GE,
∴四边形ACEG是平行四边形,
∴AG∥CE,
∴∠AGC=∠GCE=90°,
∴∠AGC+∠CGF=90°+90°=180°,
∴AG和GF在同一直线上.
点评 本题是四边形综合题目,考查了矩形的性质、全等三角形的性质、平行线的判定与性质、平行四边形的判定与性质等知识;本题综合性强,有一定难度.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
8.小强同学对本校学生完成家庭作业的时间进行了随机抽样调查,并绘成如下不完整的三个统计图表.
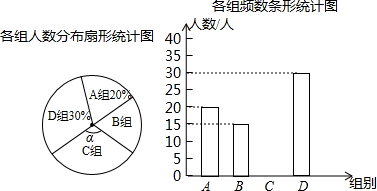
各组频数、频率统计表
(1)a=100,b=0.15,∠α=126°,并将条形统计图补充完整;
(2)若该校有学生3200人,估计完成家庭作业时间超过1小时的人数约有2080;
(3)根据以上信息,请您给校长提一条合理的建议.

各组频数、频率统计表
| 组别 | 时间 (小时) | 频数 (人) | 频率 |
| A | 0≤x≤0.5 | ||
| B | 0.5<x≤1 | b | |
| C | 1<x≤1.5 | ||
| D | x>1.5 | ||
| 合计 | a | 1.0 | |
(2)若该校有学生3200人,估计完成家庭作业时间超过1小时的人数约有2080;
(3)根据以上信息,请您给校长提一条合理的建议.
9. 在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AB,交AC于E.若AB=2$\sqrt{6}$,AC=2$\sqrt{5}$,线段DE的长为( )
在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AB,交AC于E.若AB=2$\sqrt{6}$,AC=2$\sqrt{5}$,线段DE的长为( )
 在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AB,交AC于E.若AB=2$\sqrt{6}$,AC=2$\sqrt{5}$,线段DE的长为( )
在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AB,交AC于E.若AB=2$\sqrt{6}$,AC=2$\sqrt{5}$,线段DE的长为( )| A. | 2.5 | B. | 2.4 | C. | $\sqrt{6}$ | D. | $\sqrt{5}$ |
13.阅读下列材料:
社会消费品零售总额是指批发和零售业,住宿和餐饮业以及其他行业直接售给城乡居民和社会集团的消费品零售额,在各类与消费有关的统计数据中,社会消费品零售总额是表现国内消费需求最直接的数据.
2012年,北京市全年实现社会消费品零售总额7702.8亿元,比上一年增长11.6%,2013年,全年实现社会消费品零售总额8375.1亿元,比上一年增长8.7%,2014年,全年实现社会消费品零售总额9098.1亿元,比上一年增长8.6%,2015年,全年实现社会消费品零售总额10338亿元,比上一年增长7.3%.
2016年,北京市实现市场总消费19926.2亿元,比上一年增长了8.1%,其中实现服务性消费8921.1亿元,增长10.1%;实现社会消费品零售总额11005.1亿元,比上一年增长了6.5%.
根据以上材料解答下列问题:
(1)补全统计表:
2012-2016年北京市社会消费品零售总额统计表
(2)选择适当的统计图将2012-2016年北京市社会消费品零售总额比上一年的增长率表示出来,并在图中表明相应数据;
(3)根据以上信息,估计2017年北京市社会消费品零售总额比上一年的增长率约为5.45%,你的预估理由是从2014到2016年北京市社会消费品零售总额比上一年的增长率的平均每年下降1.05%.
社会消费品零售总额是指批发和零售业,住宿和餐饮业以及其他行业直接售给城乡居民和社会集团的消费品零售额,在各类与消费有关的统计数据中,社会消费品零售总额是表现国内消费需求最直接的数据.
2012年,北京市全年实现社会消费品零售总额7702.8亿元,比上一年增长11.6%,2013年,全年实现社会消费品零售总额8375.1亿元,比上一年增长8.7%,2014年,全年实现社会消费品零售总额9098.1亿元,比上一年增长8.6%,2015年,全年实现社会消费品零售总额10338亿元,比上一年增长7.3%.
2016年,北京市实现市场总消费19926.2亿元,比上一年增长了8.1%,其中实现服务性消费8921.1亿元,增长10.1%;实现社会消费品零售总额11005.1亿元,比上一年增长了6.5%.
根据以上材料解答下列问题:
(1)补全统计表:
2012-2016年北京市社会消费品零售总额统计表
| 年份 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 |
| 社会消费品零售总额(单位:亿元) | 7702.8 | 8375.1 | 9098.1 | 10338 | 11005.1 |
(3)根据以上信息,估计2017年北京市社会消费品零售总额比上一年的增长率约为5.45%,你的预估理由是从2014到2016年北京市社会消费品零售总额比上一年的增长率的平均每年下降1.05%.
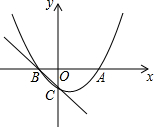 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与y轴相交于C,与x轴帕交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与y轴相交于C,与x轴帕交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).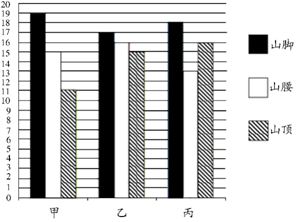 甲,乙,丙三种作物,分别在山脚,山腰和山顶三个试验田进行试验,每个试验田播种二十粒种子,农业专家将每个试验田成活的种子个数统计如条形统计图,如图所示,下面有四个推断:
甲,乙,丙三种作物,分别在山脚,山腰和山顶三个试验田进行试验,每个试验田播种二十粒种子,农业专家将每个试验田成活的种子个数统计如条形统计图,如图所示,下面有四个推断: