��Ŀ����
��֪����ΪA(1,5)��������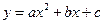 ������B(5,1).
������B(5,1).(1)�������ߵĽ���ʽ;
(2)��ͼ��1��,��C,D�ֱ���
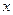 �ᡢ
�ᡢ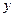 ���ϵ��������㣬���ı���ABCD�ܳ�����Сֵ��
���ϵ��������㣬���ı���ABCD�ܳ�����Сֵ����3���ڣ�2���У����ı���ABCD���ܳ���Сʱ����ֱ��CD.���P(
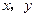 )(
)(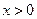 )��ֱ��
)��ֱ��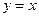 �ϵ�һ�����㣬Q��OP���е㣬��PQΪб�߰�ͼ��2����ʾ�������ֱ��������PRQ.
�ϵ�һ�����㣬Q��OP���е㣬��PQΪб�߰�ͼ��2����ʾ�������ֱ��������PRQ.�ٵ���PBR��ֱ��CD�й�����ʱ,��
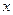 ��ȡֵ��Χ��
��ȡֵ��Χ�����ڢٵ������£��ǡ�PBR���COD�Ĺ������ֵ����ΪS.��S����
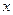 �ĺ�����ϵʽ������S�����ֵ��
�ĺ�����ϵʽ������S�����ֵ��
�⣺��1���������ߵĶ���ΪA��1��5����

���������ߵĽ���ʽΪ ��
��
����B��5��1�����룬�� ��
��
��� ��
��
��
��2����A����y��ĶԳƵ� ����B����x��ĶԳƵ�
����B����x��ĶԳƵ� ����Ȼ
����Ȼ ��
��
��ͼ(5.1)������ �ֱ�x�ᡢy����C��D���㣬
�ֱ�x�ᡢy����C��D���㣬
�� ��
��
���ʱ�ı���ABCD���ܳ���С����Сֵ���� ��
��
�� ��
��
��
�ı���ABCD�ܳ��ĵ���СֵΪ ��
��
��3���ٵ�B����x��ĶԳƵ�B�䣨 ������A����y��ĶԳƵ�A�䣨��1��5��������A��B�䣬��x�ᣬy�ύ��C��D�㣬
������A����y��ĶԳƵ�A�䣨��1��5��������A��B�䣬��x�ᣬy�ύ��C��D�㣬
��CD�Ľ���ʽΪ�� ��
��
���� ��
��
�ã�
�ߵ�P��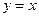 �ϣ���Q��OP���е㣬
�ϣ���Q��OP���е㣬
��Ҫʹ����ֱ����������ֱ��CD�й����㣬�� ��
��
��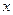 ��ȡֵ��Χ�ǣ�
��ȡֵ��Χ�ǣ� ��
��
����ͼ��


��E��2��2������EP=EQʱ�� ���ã�
���ã� ��
��
�� ʱ��
ʱ��

�� ʱ��
ʱ�� ��
��
�� ʱ��
ʱ��
�� ʱ��
ʱ�� ��
��
�� �����ֵΪ��
�����ֵΪ�� ������:
������:
��

���������ߵĽ���ʽΪ
 ��
������B��5��1�����룬��
 ��
�����
 ��
����

��2����A����y��ĶԳƵ�
 ����B����x��ĶԳƵ�
����B����x��ĶԳƵ� ����Ȼ
����Ȼ ��
��
��ͼ(5.1)������
 �ֱ�x�ᡢy����C��D���㣬
�ֱ�x�ᡢy����C��D���㣬��
 ��
��
���ʱ�ı���ABCD���ܳ���С����Сֵ����
 ��
����
 ��
��
��

�ı���ABCD�ܳ��ĵ���СֵΪ
 ��
����3���ٵ�B����x��ĶԳƵ�B�䣨
 ������A����y��ĶԳƵ�A�䣨��1��5��������A��B�䣬��x�ᣬy�ύ��C��D�㣬
������A����y��ĶԳƵ�A�䣨��1��5��������A��B�䣬��x�ᣬy�ύ��C��D�㣬��CD�Ľ���ʽΪ��
 ��
������
 ��
���ã�

�ߵ�P��
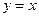 �ϣ���Q��OP���е㣬
�ϣ���Q��OP���е㣬��Ҫʹ����ֱ����������ֱ��CD�й����㣬��
 ��
����
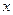 ��ȡֵ��Χ�ǣ�
��ȡֵ��Χ�ǣ� ��
������ͼ��


��E��2��2������EP=EQʱ��
 ���ã�
���ã� ��
����
 ʱ��
ʱ��

��
 ʱ��
ʱ�� ��
����
 ʱ��
ʱ��
��
 ʱ��
ʱ�� ��
����
 �����ֵΪ��
�����ֵΪ�� ������:
������:��

��ϰ��ϵ�д�
 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
�����Ŀ
 ��ͼ����֪����ΪP��������
��ͼ����֪����ΪP��������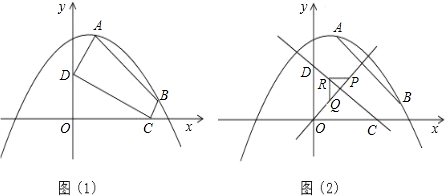
 ��ͼ����֪����ΪC��������y=ax2-4ax+c�����㣨-2��0������y�ύ�ڵ�A��0��3������B���������ϵĵ㣬������AB��x�ᣮ
��ͼ����֪����ΪC��������y=ax2-4ax+c�����㣨-2��0������y�ύ�ڵ�A��0��3������B���������ϵĵ㣬������AB��x�ᣮ ��ͼ����֪����ΪP��������
��ͼ����֪����ΪP�������� ������A��-3��6������x�ύ��B��-1��0����C���㣮
������A��-3��6������x�ύ��B��-1��0����C���㣮