��Ŀ����
����Ŀ���ۺ���ʵ��
��ֽ��ͬѧ��ϲ�����ֹ��֮һ��ͨ����ֽ���Ǽȿ��Եõ�����������ͼ�Σ�ͬʱ��ֽ�Ĺ��̻��̺��ŷḻ����ѧ֪ʶ����һ�ۣ��ѱ߳�Ϊ![]() ��������ֽƬ
��������ֽƬ![]() ���ۣ�ʹ��
���ۣ�ʹ��![]() ��
��![]() �غϣ�չ����õ��ۺ�
�غϣ�չ����õ��ۺ�![]() ����ͼ�٣���
����ͼ�٣���![]() Ϊ
Ϊ![]() ��һ�㣬��������ֽƬ
��һ�㣬��������ֽƬ![]() ��ֱ��
��ֱ��![]() �۵���ʹ��
�۵���ʹ��![]() ����
����![]() �ϵĵ�
�ϵĵ�![]() ����չ��������
����չ��������![]() ��
��![]() ��
��![]() ����ͼ��
����ͼ��
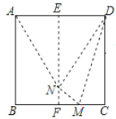
ͼ�� ͼ��
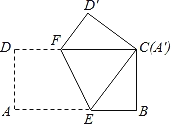
��һ����һ���һ����
��1��ͼ���У�![]() _______���߶�
_______���߶�![]() _______��
_______��
��2��ͼ���У����ж�![]() ����״��������֤����
����״��������֤����
��һ������һ�ۣ���ͼ���е�![]() ��������������ֱ��
��������������ֱ��![]() �۵���ʹ��
�۵���ʹ��![]() ���ڵ�
���ڵ�![]() �����ֱ�õ�ͼ�ۡ�ͼ�ܣ�
�����ֱ�õ�ͼ�ۡ�ͼ�ܣ�
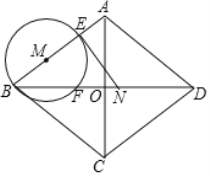
��������һ��
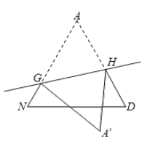
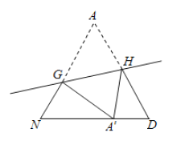
ͼ�� ͼ��
��3��ͼ������Ӱ���ֵ��ܳ�Ϊ_______��
��4��ͼ���У���![]() ����
����![]() _______�㣮
_______�㣮
��5��ͼ���е����������Σ�����ȫ�������Σ�����_______�ԣ�
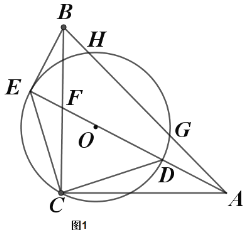
��6����ͼ�ܵ�![]() ���ڱ�
���ڱ�![]() �ϣ���
�ϣ���![]() _______����
_______����![]() _______�ú�
_______�ú�![]() ��
��![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
���𰸡���1��![]() ��
��![]() ��2��
��2��![]() �ǵȱ������Σ�3��
�ǵȱ������Σ�3��![]() ����4��
����4��![]() ��5��
��5��![]() ��6��
��6��![]()
��������
��1�����۵������ʵã��ı���![]() �Ǿ��Σ��ó�
�Ǿ��Σ��ó�![]() ��
��![]() ��
��![]() �����۵������ʵó�
�����۵������ʵó�![]() ��
��![]() ���ó�
���ó�![]() ���ó�
���ó�![]() ��
��![]() �����
�����![]() ��
��![]() ��
��
��2��֤��![]() �ó�
�ó�![]() �����ɵó�
�����ɵó�![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��3�����۵������ʵó�![]() ��
��![]() ���ó�ͼ������Ӱ���ֵ��ܳ�
���ó�ͼ������Ӱ���ֵ��ܳ�![]() ���ܳ�
���ܳ�![]() ��
��
��4�����۵������ʵó�![]() ��
��![]() �����
�����![]() ���ó�
���ó�![]() �����ɵó������
�����ɵó������
��5��֤��![]() �����ɵó����ۣ�
�����ɵó����ۣ�
��6����![]() ����
����![]() ��
��![]() ֤��
֤��![]() ���ó�
���ó�![]() ����
����
![]() ��
��![]() ����
����![]() ��
��![]() ���ó�
���ó�![]() ����ã�
����ã�![]() ���ó�
���ó�![]() ��
��
�⣺��1�����۵������ʵã��ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
![]()
![]() ��
��![]() ��
��![]() ��
��
![]() ��������ֽƬ
��������ֽƬ![]() ��ֱ��
��ֱ��![]() �۵���ʹ��
�۵���ʹ��![]() ����
����![]() �ϵĵ�
�ϵĵ�![]() ����
����
![]()
![]() ��
��![]() ��
��
![]()
![]() ��
��
![]()
![]() ��
��![]() ��
��
![]()
![]() ��
��![]() ��
��
�ʴ�Ϊ![]() ��
��![]() ��
��
��2��![]() �ǵȱ������Σ��������£�
�ǵȱ������Σ��������£�
��![]() ��
��![]() ��
�� ��
��
![]()
![]() ��
��
![]()
![]() ��
��
![]()
![]() ��
��
![]()
![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��3���߽�ͼ���е�![]() ��ֱ��
��ֱ��![]() �۵���ʹ��
�۵���ʹ��![]() ���ڵ�
���ڵ�![]() ����
����
![]()
![]() ��
��![]() ��
��
![]() ͼ������Ӱ���ֵ��ܳ�
ͼ������Ӱ���ֵ��ܳ�![]() ���ܳ�
���ܳ�![]() ��
��
�ʴ�Ϊ![]() ��
��
��4��![]() ��ͼ���е�
��ͼ���е�![]() ��ֱ��
��ֱ��![]() �۵���ʹ��
�۵���ʹ��![]() ���ڵ�
���ڵ�![]() ����
����
![]()
![]() ��
��![]() ��
��
![]()
![]() ��
��
![]()
![]() ��
��
![]()
![]() �㣬
�㣬
![]()
![]() ��
��
�ʴ�Ϊ![]() ��
��
��5����ͼ�ۣ�
![]()
![]() ��
��
![]() ��
��![]() ��
��
![]()
![]() ��
��
![]()
![]()
![]() ͼ���е����������Σ�����ȫ�������Σ�����
ͼ���е����������Σ�����ȫ�������Σ�����![]() �ԣ�
�ԣ�

ͼ��
�ʴ�Ϊ![]() ��
��
��6����![]() ����
����![]() ��
��![]() ��
��
![]()
![]() ��
��
![]()
![]() ��
��
![]()
![]() ��
��
![]()
![]() ��
��
![]()
![]() ��
��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
![]()
![]() ��
��
��ã�![]() ��
��
��![]()
![]() ��
��
�ʴ�Ϊ![]() ��
��

 53���ò�ϵ�д�
53���ò�ϵ�д�����Ŀ��ij�Ҿ��̳��ƻ�����ij�ֲ��������ν������ۣ��й���Ϣ���±���
ԭ���ۣ�Ԫ/�ţ� | ���ۼۣ�Ԫ/�ţ� | �����ۼۣ�Ԫ/�ף� | |
���� | a | 380 | 940 |
���� |
| 160 |
��֪��600Ԫ�����IJ�����������1300Ԫ�����IJ���������ͬ��
��1�������a��ֵ��
��2�����̳��ƻ��������ε������Dz���������5������20�ţ��Ҳ����Ͳ��ε�������������200�ţ�����һ��IJ������ף�һ�Ų��������Ų������һ�ף����ۣ�������������������۷�ʽ���ۣ������������������ܻ�����������������Ƕ��٣�
����Ŀ������Ϣ���ٷ�չ����ᣬ����Ϣ�������ѳ�Ϊ�����������Ҫ��ɲ��֣�ij��У��֯����С�������е�һ�����������ȡ���ּ�ͥ������ÿ��������Ϣ���ѵĽ������������������²�����ͳ�Ʊ���ͳ��ͼ����ͼ������֪![]() ��
��![]() ���黧��Ƶ���˷�ͼ�ĸ߶ȱ�Ϊ1��5��
���黧��Ƶ���˷�ͼ�ĸ߶ȱ�Ϊ1��5��
����Ϣ���Ѷ����ͳ�Ʊ�
��� | ���Ѷ�/Ԫ |
|
|
|
|
|
|
|
|
|
|
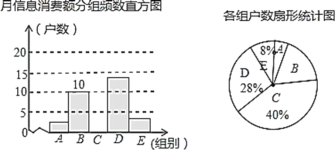
����ͼ����������ݽ���������⣺
��1����ν��ܵ������_________����
��2���㲹ȫƵ��ֱ��ͼ��
��3���Ը�������ֵ�������������Ϣ���Ѷ��ƽ�������������С���ȡ��ͥ������Ϣ���Ѷ��ƽ������
��4������������2000��ס�������������Ϣ���Ѷ����200Ԫ�Ļ����Ƕ��٣�