题目内容
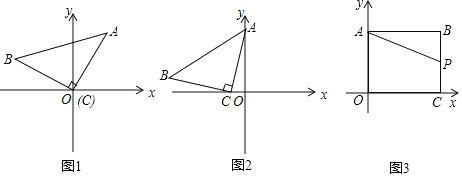
【题目】如图，在平面直角坐标系中，点
，点
，点P是直线
上一点，且
，则点P的坐标为______．
【答案】
【解析】
由于题目中给出
，则可考虑构造等腰直角三角形进行解决，将AB顺时针旋转
得到线段BC，求出点C的坐标，连接AC，则AC与BP的交点M即为线段AC的中点，可求出M的坐标，则直线BP的解析式亦可求的，再将直线
与直线BP的解析式联立成方程组，即可求出点P的坐标．
如图所示，
将线段AB绕点B顺时针旋转得到线段BC，则点C的坐标为
，
由于旋转可知，
为等腰直角三角形，令线段AC和线段BP交于点M，则M为线段AC的中点，
所以点M的坐标为
，又B为
，设直线BP为
，将点B和点M代入可得
，
解得
，
，可得直线BP为
，由于点P为直线BP和直线
的交点，
则由
解得
，所以点P的坐标为，
故答案为．
练习册系列答案
相关题目
