��Ŀ����
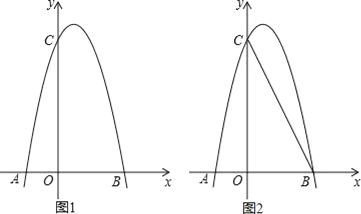
����Ŀ����ͼ����ƽ��ֱ��Щ��ϵ�У����κ���y��ax2+bx��![]() ��ͼ����A����1��0����C��2��0������y�ύ�ڵ�B����Գ�����x�ύ�ڵ�D��
��ͼ����A����1��0����C��2��0������y�ύ�ڵ�B����Գ�����x�ύ�ڵ�D��
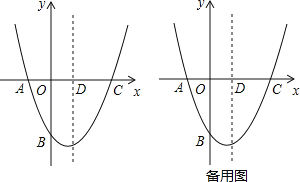
��1������κ����ı���ʽ���䶥������ꣻ
��2����PΪy���ϵ�һ�����㣬����PD����![]() PB+PD����Сֵ��
PB+PD����Сֵ��
��3��M��x��t��Ϊ�����߶Գ�����һ�����㣬��ƽ���ڴ��ڵ�N��ʹ����A��B��M��NΪ������ı���Ϊ���Σ��������ĵ�N������ ������
���𰸡���1��![]() �������ߵĶ�������Ϊ��
�������ߵĶ�������Ϊ��![]() ������2����СֵΪ
������2����СֵΪ![]() ����3��5��
����3��5��
��������
(1)��A��C������������y=ax2+bx��![]() �����ô���ϵ��������������κ����ı���ʽ�������õ��䶥�����ꣻ
�����ô���ϵ��������������κ����ı���ʽ�������õ��䶥�����ꣻ
(2)����AB����DH��AB��H����OB��P����ʱ![]() PB+PD��С����Сֵ�����߶�DH�����DH���ɣ�
PB+PD��С����Сֵ�����߶�DH�����DH���ɣ�
(3)����A��B��M��NΪ������ı���Ϊ����ʱ�����������������AΪԲ��ABΪ�뾶������Գ������������㣬��ʱAM=AB������BΪԲ��ABΪ�뾶������Գ������������㣬��ʱBM=AB�����߶�AB�Ĵ�ֱƽ������Գ�����һ�����㣬��ʱAM=BM����M��ĸ�����ɵó���N�ĸ�����5����
(1)�߶��κ���![]() ��ͼ����A(��1��0)C(2��0)��
��ͼ����A(��1��0)C(2��0)��
�� ��
��
��ã� ��
��
����κ����ı���ʽΪ![]() ��
��
��y=![]() ��
��
�������ߵĶ�������Ϊ(![]() )��
)��
(2)��ͼ������AB����DH��AB��H����OB��P����ʱ![]() PB+PD��С��
PB+PD����

���ɣ���OA=1��OB=![]() ��
��
��![]() ��
��
��![]() ��
��
���ABO=30����
��PH=![]() PB��
PB��
��![]() PB+PD=PH+PD=DH��
PB+PD=PH+PD=DH��
���ʱ![]() PB+PD���(���߶����);
PB+PD���(���߶����);
�������ߵĶ�������Ϊ(![]() )��
)��
��![]() ��
��
�ߡ�ABO=30����
���HAD=60����
��Rt��ADH�У��ߡ�AHD=90����AD=![]() ����HAD=60����
����HAD=60����
��sin60��=![]() ��
��
��DH=![]() ��
��
��![]() PB+PD����СֵΪ
PB+PD����СֵΪ![]() ��
��
(3)����AΪԲ��ABΪ�뾶��������ΪAB��AD���ʴ�ʱԲ����Գ������������㣬��AM=AB����M�������������������������N����������
����BΪԲ��ABΪ�뾶��������Ϊ![]() ���ʴ�ʱԲ����Գ������������㣬��BM=AB����M������������������������N����������
���ʴ�ʱԲ����Գ������������㣬��BM=AB����M������������������������N����������
���߶�AB�Ĵ�ֱƽ������Գ�����һ�����㣬��ʱAM=BM����ΪM����һ������������������N����һ����
������������N�㹲��5����
�ʴ�Ϊ��5��

 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�