题目内容
【题目】问题呈现：下图是小明复习全等三角形时遇到的一个问题并引发的思考，请帮助小明完成以下学习任务．
请根据小明的思路，结合图①，写出完整的证明过程．结论应用：
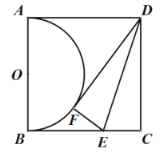
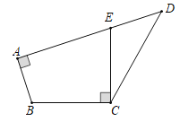
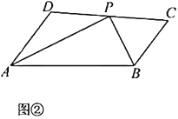
（1）如图②，在四边形
中，
，
的平分线和
的平分线交于
边上点
．求证：
；
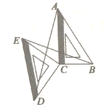
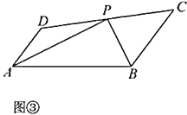
（2）在（1）的条件下，如图③，若
，
．当
有一个内角是
时，
的面积是 ．
【答案】问题呈现：见解析；结论应用：（1）见解析；（2）
或8
【解析】
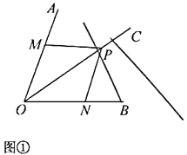
问题呈现：由“SAS”可证△MOP≌△NOP，可得PM＝PN；
结论应用：（1）在AB上截取AE＝AD，连接PE，由“SAS”可证△ADP≌△AEP，△BPC≌△BPE，可得PD＝PE＝PC；（2）延长AP，BC交于点H，由“ASA”可证△ADP≌△HCP，可得CP＝DP，AD＝CH，S△ADP＝S△CPH，分三种情况讨论，由角平分线的性质和锐角三角函数可求解．
问题呈现：
证明：∵
平分
，
∴
．
在
和
中，
．
∴
．
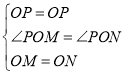结论应用：
在
上截取
，
∵
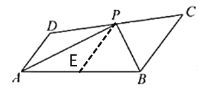
平分
，
∴
，
∵
，
∴
．
∴
．
∵
，
∴
，
∵
平分
，
∴
．
∵
．
∴
．
∴
．
∴
．
（2）由（1）可证∠D＝∠AEP，∠PCB＝∠PEB，
∵∠AEP+∠PEB＝180°，
∴∠PCB+∠D＝180°，
∴AD∥BC，
∵AB＝10，tan∠PAB＝
＝
，
∴PA＝2PB，
∵PA2+PB2＝AB2，
∴PB＝2
，PA＝4，
如图③，延长AP，BC交于点H，
∵AD∥BC，
∴∠DAP＝∠H，
∴∠H＝∠BAP，
∴AB＝BH＝10，
又∵PB平分∠ABC，
∴BP⊥AP，AP＝PH＝4，
∵∠DAP＝∠H，AP＝PH，∠DPA＝∠CPH，
∴△ADP≌△HCP（ASA），
∴CP＝DP，AD＝CH，S△ADP＝S△CPH，
若∠PBC＝45°时，则∠PBC＝∠H＝45°，
∴PB＝PH（不合题意舍去），
若∠BPC＝45°时，则∠HPC＝∠BPC＝45°，
如图④，过点C作CN⊥BP于N，CM⊥PH于M，
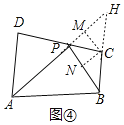
∴CM＝CN，
∵S△PBH＝×BP×PH＝×BP×CN+×PH×CM，
∴CM＝CN＝
，
∴S△PCH＝×4×
＝＝S△ADP；
若∠PCB＝45°时，
如图⑤，过点P作PF⊥BC于F，
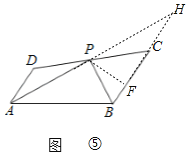
∵∠PAB＝∠H，
∴tanH＝tan∠PAB＝，
∴
，
∴FH＝2PF，
∵PF2+FH2＝PH2＝80，
∴PF＝4，FH＝8，
∵PF⊥BC，∠BCP＝45°，
∴∠PCB＝∠FPC＝45°，
∴CF＝PF＝4，
∴CH＝4，
∴S△ADP＝S△CPH＝×4×4＝8，
故答案为：8或．
