题目内容
 我国宋朝数学家杨辉在他的著作《详解九章算法》中提出如表,此表揭示了(a+b)n(n为非负整数)展开式的各项系数的规律.例如:(a+b)0=1,它只有一项,系数为1;(a+b)1=a+b,它有两项,系数分别为1,1;(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1;(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1;
我国宋朝数学家杨辉在他的著作《详解九章算法》中提出如表,此表揭示了(a+b)n(n为非负整数)展开式的各项系数的规律.例如:(a+b)0=1,它只有一项,系数为1;(a+b)1=a+b,它有两项,系数分别为1,1;(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1;(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1;…
根据以上规律,请写出(a+b)4的展开式=
考点:规律型:数字的变化类
专题:
分析:观察可得(a+b)n(n为非负整数)展开式的各项系数的规律:首尾两项系数都是1,中间各项系数等于(a+b)n-1相邻两项的系数和.因此可得(a+b)4的各项系数分别为1、(1+3)、(3+3)、(3+1)、1,即:1、4、6、4、1.
解答:解:(a+b)4=a4+4a3b+6a2b2+4ab3+b4.有5项,
(a+b)4的各项系数分别为1、(1+3)、(3+3)、(3+1)、1,即:1、4、6、4、1.
故答案为:a4+4a3b+6a2b2+4ab3+b4;5;1、4、6、4、1.
(a+b)4的各项系数分别为1、(1+3)、(3+3)、(3+1)、1,即:1、4、6、4、1.
故答案为:a4+4a3b+6a2b2+4ab3+b4;5;1、4、6、4、1.
点评:此题考查数字的变化规律,从简单入手,找出规律,利用规律解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 将一张矩形纸对折再对折,然后沿着如图中的虚线剪下,打开,这个图形一定是一个(
将一张矩形纸对折再对折,然后沿着如图中的虚线剪下,打开,这个图形一定是一个(| A、三角形 | B、矩形 |
| C、菱形 | D、正方形 |
 用平面截下列几何体,相应的截面形状是( )
用平面截下列几何体,相应的截面形状是( )A、 |
B、 |
C、 |
 如图,是一个长方体纸盒的平面展开图,每个面都标有字母.请根据下面的要求回答问题:
如图,是一个长方体纸盒的平面展开图,每个面都标有字母.请根据下面的要求回答问题: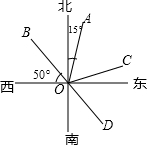 如图,OA的方向是北偏东15°,OB的方向是西偏北50°.
如图,OA的方向是北偏东15°,OB的方向是西偏北50°. 如图,x轴、y轴分别平分∠DBC、∠EAD,求∠AED+∠BCD的值.
如图,x轴、y轴分别平分∠DBC、∠EAD,求∠AED+∠BCD的值.