题目内容
 如图,ABCD是一个边长为1的正方形,U、V分别是AB、CD上的点,AV与DU相交于点P,BV与CU相交于点Q.求四边形PUQV面积的最大值.
如图,ABCD是一个边长为1的正方形,U、V分别是AB、CD上的点,AV与DU相交于点P,BV与CU相交于点Q.求四边形PUQV面积的最大值.
分析:连接UV,根据等底等高的三角形的面积相等,推出S四边形PUQV=S△APD+S△BQC,再利用面积公式求出面积,进一步根据不等式的性质即可求出四边形PUQV面积的最大值.
解答: 解:连接UV,
解:连接UV,
∵正方形ABCD,
∴AB∥CD,
根据等底等高的三角形的面积相等得到:S△APD=S△UVP,S△QUV=S△BQC,
∴S四边形PUQV=S△APD+S△BQC,
过P做PE⊥AD于E,过Q做QF⊥BC于F,
设:PE=x,QF=y,
∴S四边形PUQV=
(x+y),
设AU=a,DV=b,
则
+
=DE+AE=1,
故x=
,
同理y=
=
,
∴S四边形PUQV=
[
+
],
=
=
≤
=
=
(因为(a-b)2≥0)2+b,
等号当且仅当a=b时成立,
故四边形PUQV面积最大值是
.
 解:连接UV,
解:连接UV,∵正方形ABCD,
∴AB∥CD,
根据等底等高的三角形的面积相等得到:S△APD=S△UVP,S△QUV=S△BQC,
∴S四边形PUQV=S△APD+S△BQC,
过P做PE⊥AD于E,过Q做QF⊥BC于F,
设:PE=x,QF=y,
∴S四边形PUQV=
| 1 |
| 2 |
设AU=a,DV=b,
则
| x |
| a |
| x |
| b |
故x=
| ab |
| a+b |
同理y=
| (1-a)(1-b) |
| (1-a)+(1-b) |
| (1-a)(1-b) |
| 2-a-b |
∴S四边形PUQV=
| 1 |
| 2 |
| ab |
| a+b |
| (1-a)(1-b) |
| 2-a-b |
=
| (a+b)-(a2+b2) |
| 2(a+b)(2-a-b) |
=
| 2(a+b)-a2-b2-(a2+b2) |
| 4(a+b)(2-a-b) |
| 2(a+b)-a2-b2-2ab |
| 4(a+b)(2-a-b) |
| (a+b)(2-a-b) |
| 4(a+b)(2-a-b) |
| 1 |
| 4 |
等号当且仅当a=b时成立,
故四边形PUQV面积最大值是
| 1 |
| 4 |
点评:本题主要考查了面积及等积变换,三角形的面积不等式的性质等知识点,解此题的关键是利用不等式的性质求最大值,此题难度较大.

练习册系列答案
相关题目
 (1997•山东)如图,ABCD是一个正方形,P、Q是正方形外两点,且△APD和△BCQ是等边三角形,则∠PQD的正切值是( )
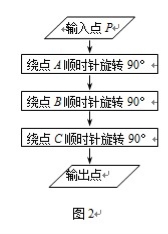
(1997•山东)如图,ABCD是一个正方形,P、Q是正方形外两点,且△APD和△BCQ是等边三角形,则∠PQD的正切值是( ) 如图1正方形ABCD是一个8行8列网格电子屏的示意图,其中每个小正方形的边长为1.位于AD中点处的光点P按图2的程序移动.
如图1正方形ABCD是一个8行8列网格电子屏的示意图,其中每个小正方形的边长为1.位于AD中点处的光点P按图2的程序移动.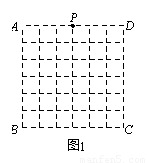
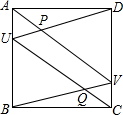 如图,ABCD是一个边长为1的正方形,U、V分别是AB、CD上的点,AV与DU相交于点P,BV与CU相交于点Q.求四边形PUQV面积的最大值.
如图,ABCD是一个边长为1的正方形,U、V分别是AB、CD上的点,AV与DU相交于点P,BV与CU相交于点Q.求四边形PUQV面积的最大值.