Question

某广场地面铺满了边长为36 cm的正六边形地砖（局部图如左下图所示），现在向上抛掷半径为6

3

cm的圆碟，求圆碟落地后与地砖间的间隙不相交的概率．

Answer 1

分析：欲使圆碟不压地砖间的间隙，则圆碟的圆心必须落在与地砖同中心，且边与地砖边彼此平行，距离为6

3

cm的小正六边形内，找到小正六边形的面积占大正六边形面积的多少即可．

解答：解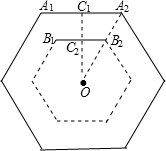：如图，作OC₁⊥A₁A₂，且C₁C₂=6

3

cm．
∵A₁A₂=A₂O=36 A₂C₁=18，
∴C₁O=

3

2

A₂O=18

3

，
则C₂O=C₁O-C₁C₂=12

3

．
∵C₂O=

3

2

B₂O，
∴B₂O=

2

3

C₂O=

2

3

×12

3

=24，
∵B₁B₂=B₂O，
∴小正六边形的边长为24cm．
∴所求概率为P=

小正六边形的面积

正六边形地砖面积

=

B1 B 2 2

A1 A 2 2

=

242

362

=

4

9

．

点评：用到的知识点为：相似多边形的面积比等于相似比的平方；求相应概率求得相应面积比即可．