题目内容
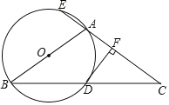
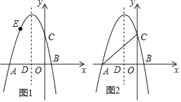
【题目】如图所示,AC⊥AB,![]() ,AC=2,点D是以AB为直径的半圆O 上一动点,DE⊥CD交直线AB于点E,设
,AC=2,点D是以AB为直径的半圆O 上一动点,DE⊥CD交直线AB于点E,设![]() .
.

(1)当![]() 时,求弧BD的长;
时,求弧BD的长;
(2)当![]() 时,求线段BE的长;
时,求线段BE的长;
(3)若要使点E在线段BA的延长线上,则![]() 的取值范围是 .(直接写出答案)
的取值范围是 .(直接写出答案)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)60°<α<90°.
;(3)60°<α<90°.
【解析】
(1)首先连接OD,由圆周角定理,可求得∠DOB的度数,又由⊙O的直径为2![]() ,即可求得其半径,然后由弧长公式,即可求得答案;
,即可求得其半径,然后由弧长公式,即可求得答案;
(2)首先证得△ACD∽△BED,然后由相似三角形的对应边成比例,可得![]() =
=![]() ,继而求得答案;
,继而求得答案;
(3)首先求得A与E重合时α的度数,则可求得点E在线段BA的延长线时,α的取值范围.
解:(1)
如图,连接OD,
∵α=20°,∴∠DOB=2α=40°,
∵AB=2![]() ,
,
∴⊙O的半径为:![]() ,
,
∴![]() 的长为
的长为![]() =
=![]() ;
;
(2)∵AB是⊙O的直径,
∴∠ADB=90°,∵α=30°,∴∠B=60°,∵AC⊥AB,DE⊥CD,
∴∠CAB=∠CDE=90°,∴∠CAD=90°﹣α=60°,
∴∠CAD=∠B,∵∠CDA+∠ADE=∠ADE+∠BDE=90°,
∴∠CDA=∠BDE,∴△ACD∽△BED,
∴![]() =
=![]() ,∵AB=2
,∵AB=2![]() ,α=30°,
,α=30°,
∴BD=![]() AB=
AB=![]() ,∴AD=
,∴AD=![]() =3,
=3,
∴![]() =
=![]() ,∴BE=
,∴BE=![]() ;
;
(3)
如图,当E与A重合时,
∵AB是直径,AD⊥CD,
∴∠ADB=∠ADC=90°,
∴C,D,B共线,
∵AC⊥AB,
∴在Rt△ABC中,AB=2![]() ,AC=2,
,AC=2,
∴tan∠ABC=![]() =
=![]() ,
,
∴∠ABC=30°,
∴α=∠DAB=90°-∠ABC=60°,
当E′在BA的延长线上时,如图,可得∠D′AB>∠DAB=60°,
∵0°<α<90°,
∴α的取值范围是:60°<α<90°.
故答案为:60°<α<90°.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目