题目内容
已知⊙O的半径为5,弦AB的长为5
,则圆心角∠AOB= .
| 2 |
考点:垂径定理,等腰直角三角形
专题:计算题
分析:根据题意画出图形,过O作OC垂直于AB,利用垂径定理得到C为AB的中点,在直角三角形AOC中,利用锐角三角函数定义求出sin∠AOC的值,确定出∠AOC的度数,即可求出∠AOB的度数.
解答: 解:根据题意画出图形,过O作OC⊥AB,得到C为AB的中点,
解:根据题意画出图形,过O作OC⊥AB,得到C为AB的中点,
∴AC=BC=
AB=
,
在Rt△AOC中,OA=5,
∴sin∠AOC=
=
,即∠AOC=45°,
则∠AOB=∠AOC=90°.
故答案为:90°
 解:根据题意画出图形,过O作OC⊥AB,得到C为AB的中点,
解:根据题意画出图形,过O作OC⊥AB,得到C为AB的中点,∴AC=BC=
| 1 |
| 2 |
5
| ||
| 2 |
在Rt△AOC中,OA=5,
∴sin∠AOC=
| AC |
| OA |
| ||
| 2 |
则∠AOB=∠AOC=90°.
故答案为:90°
点评:此题考查了垂径定理,勾股定理,熟练掌握垂径定理是解本题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
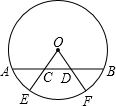 如图,在⊙O中,E,F为
如图,在⊙O中,E,F为