题目内容
9.解不等式组$\left\{{\begin{array}{l}{2x<5}\\{3({x+2})≥x+4}\end{array}}\right.$并在数轴上表示解集.分析 分别求出每一个不等式的解集,根据口诀:大小小大中间找,确定不等式组的解集,再根据“大于向右,小于向左,包括端点用实心,不包括端点用空心”的原则在数轴上将解集表示出来.
解答 解:解不等式2x<5,得:x<$\frac{5}{2}$,
解不等式3(x+2)≥x+4,得:x≥-1,
∴不等式组的解集为:-1≤x<$\frac{5}{2}$,
将不等式解集表示在数轴上如图:
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.我国2016年第一季度GDP总值经初步核算大约为159000亿元,数据159000用科学记数法表示为( )
| A. | 1.59×104 | B. | 1.59×105 | C. | 1.59×104 | D. | 15.9×104 |
4.中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数.如果收入100元记作+100元.那么-80元表示( )
| A. | 支出20元 | B. | 收入20元 | C. | 支出80元 | D. | 收入80元 |
7.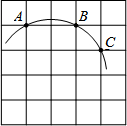 如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是( )
如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是( )
 如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是( )
如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是( )| A. | (0,0) | B. | (-1,1) | C. | (-1,0) | D. | (-1,-1) |
 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连结BE,CD,F为BE的中点,连结AF,求证:CD=2AF.
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连结BE,CD,F为BE的中点,连结AF,求证:CD=2AF.