题目内容
 如图,正△ABC中,点M、N分别在AB、AC上,且AN=BM,BN与CM相交于点O,若S△ABC=7,S△OBC=2,则
如图,正△ABC中,点M、N分别在AB、AC上,且AN=BM,BN与CM相交于点O,若S△ABC=7,S△OBC=2,则 =________.
=________.
 或
或
分析:根据等边三角形的性质证明△BAN≌△CBM(SAS),然后有全等三角形的性质知S△BAN=S△CBM,最后利用“割补法”求得△AOM和△BOM面积间的数量关系列出方程,解方程即可.
解答:
 解:连接AO,设S△AOM=m,BM:MA=a:1(a>0).
解:连接AO,设S△AOM=m,BM:MA=a:1(a>0).∵AN=BM,AB=AC,
∴AN:CN=a;
在△BAN和△CBM中:
∵△ABC为正三角形,
∴AB=BC,∠BAN=∠CBM=60°,
又∵BM=AN,
∴△BAN≌△CBM(SAS),
∴S△BAN=S△CBM,
∴S△BAN-S△BOM=S△CBM-S△BOM,
∴S四边形AMON=S△BOC;
又∵S△OBC=2,
∴S四边形AMON=2;
∴S△AON=S四边形AMON-S△AOM=2-m…①
而S△ABC=7,
∴S△BOM+S△CON=S△ABC-S△BOC-S四边形AMON=3;
∵△AOM和△BOM的高相等(都是点O到AB得距离),
∴S△BOM:S△AOM=BM:AM=a,
∴S△BOM=am…②
∴S△CON=3-S△BOM=3-am,
同理,S△AON:S△CON=AN:CN=a,
∴(2-m):(3-am)=a,即2-m=3a-a2m…③
同理,S△ACM:S△BCM=AM:BM=1:a,
∴[m+(2-m)+(3-am)]:(am+2)=1:a,即(5-am):(am+2)=1:a,
∴am+2=5a-a2m…④
④-③得,(a+1)m=2a
∴m=
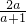 ;
; 将m值代入③式,得
2-
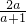 =3a-a2•
=3a-a2•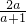 ,即(a+1)(2a-1)(a-2)=0,
,即(a+1)(2a-1)(a-2)=0,∴a=
 1,或者a=2;
1,或者a=2; 当a=
 时,
时, ;
;当a=2时,
 ;
;故答案为:
 或
或 .
.点评:本题主要考查了等边三角形的性质和全等三角形的判定及性质;判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
相关题目
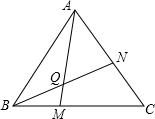
 如图,正△ABC中,点M、N分别在AB、AC上,且AN=BM,BN与CM相交于点O,若S△ABC=7,S△OBC=2,则
如图,正△ABC中,点M、N分别在AB、AC上,且AN=BM,BN与CM相交于点O,若S△ABC=7,S△OBC=2,则 如图,正△ABC中,MN∥AC,
如图,正△ABC中,MN∥AC,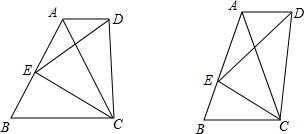 (2011•路北区一模)探究一:如图,正△ABC中,E为AB边上任一点,△CDE为正三角形,连接AD,猜想AD与BC的位置关系,并说明理由.
(2011•路北区一模)探究一:如图,正△ABC中,E为AB边上任一点,△CDE为正三角形,连接AD,猜想AD与BC的位置关系,并说明理由.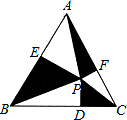 如图,正△ABC中,P为正三角形内任意一点,过P作PD⊥BC,PE⊥AB,PF⊥AC连结AP、BP、CP,如果
如图,正△ABC中,P为正三角形内任意一点,过P作PD⊥BC,PE⊥AB,PF⊥AC连结AP、BP、CP,如果