题目内容
 如图,正△ABC中,MN∥AC,
如图,正△ABC中,MN∥AC,| BM |
| AM |
| 3 |
| 2 |
| S△AOD |
| S△ABC |
| 1 |
| 5 |
| AD |
| AC |
| 1 |
| 3 |
| 1 |
| 3 |
分析:连BO交MN于F,交AC于E;由△ABC为等边三角形,MN∥AC得△BMN为等边三角形,而O为△BMN的外心,根据等边三角形的性质得到BF⊥MN,且O为△BMN的内心,则BO:OF=2,易得BE⊥AC,BO:BF=2:3①;再利用平行线分线段成比例定理得BF:BE=MB:BA=3:5,利用比例性质得BF:BE=3:5②,由①②得BO:BE=2:5,则OE:BE=3:5,然后根据三角形的面积公式和S△OAD:△ABC=1:5即可计算出AD与AC的比.
解答: 解:连BO交MN于F,交AC于E,如图,
解:连BO交MN于F,交AC于E,如图,
∵△ABC为等边三角形,MN∥AC
∴△BMN为等边三角形,
而O为△BMN的外心,
∴BF⊥MN,BO:OF=2,
∴BE⊥AC,BO:BF=2:3①,
又∵MN∥AC,
∴BF:BE=MB:BA,
而MB:AM=3:2,即有BM:AB=3:5,
∴BF:BE=3:5②,
由①②得BO:BE=2:5,
∴OE:BE=3:5,
而S△OAD=
AD•OE,S△ABC=
AC•BE,
∵S△OAD:△ABC=1:5,
∴
=
,
∴
=
.
故答案为
.
 解:连BO交MN于F,交AC于E,如图,
解:连BO交MN于F,交AC于E,如图,∵△ABC为等边三角形,MN∥AC
∴△BMN为等边三角形,
而O为△BMN的外心,
∴BF⊥MN,BO:OF=2,
∴BE⊥AC,BO:BF=2:3①,
又∵MN∥AC,
∴BF:BE=MB:BA,
而MB:AM=3:2,即有BM:AB=3:5,
∴BF:BE=3:5②,
由①②得BO:BE=2:5,
∴OE:BE=3:5,
而S△OAD=
| 1 |
| 2 |
| 1 |
| 2 |
∵S△OAD:△ABC=1:5,
∴
| AD•OE |
| AC•BE |
| 1 |
| 5 |
∴
| AD |
| AC |
| 1 |
| 3 |
故答案为
| 1 |
| 3 |
点评:本题考查了三角形外心的性质:三角形的外心到三角形三个顶点的距离相等.也考查了等边三角形的性质、平行线分线段成比例定理以及比例的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
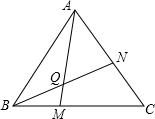
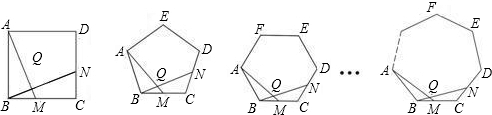
 如图,正△ABC中,点M、N分别在AB、AC上,且AN=BM,BN与CM相交于点O,若S△ABC=7,S△OBC=2,则
如图,正△ABC中,点M、N分别在AB、AC上,且AN=BM,BN与CM相交于点O,若S△ABC=7,S△OBC=2,则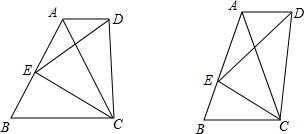 (2011•路北区一模)探究一:如图,正△ABC中,E为AB边上任一点,△CDE为正三角形,连接AD,猜想AD与BC的位置关系,并说明理由.
(2011•路北区一模)探究一:如图,正△ABC中,E为AB边上任一点,△CDE为正三角形,连接AD,猜想AD与BC的位置关系,并说明理由.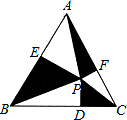 如图,正△ABC中,P为正三角形内任意一点,过P作PD⊥BC,PE⊥AB,PF⊥AC连结AP、BP、CP,如果
如图,正△ABC中,P为正三角形内任意一点,过P作PD⊥BC,PE⊥AB,PF⊥AC连结AP、BP、CP,如果