题目内容
19.已知a是不为1的有理数,我们把$\frac{1}{1-a}$称为a的差倒数.如:2的差倒数是$\frac{1}{1-2}$,-1的差倒数是$\frac{1}{1-(-1)}$=$\frac{1}{2}$.已知a1=-$\frac{1}{3}$,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2017=-$\frac{1}{3}$.分析 根据差倒数的定义分别求解,然后根据变化规律确定出3个数为一个循环组依次循环,再用2017除以3,根据商和余数的情况解答.
解答 解:a1=-$\frac{1}{3}$,
a2=$\frac{1}{1-{a}_{1}}$=$\frac{1}{1-(-\frac{1}{3})}$=$\frac{3}{4}$,
a3=$\frac{1}{1-{a}_{2}}$=$\frac{1}{1-\frac{3}{4}}$=4,
a4=$\frac{1}{1-{a}_{3}}$=$\frac{1}{1-4}$=-$\frac{1}{3}$,
…,
依此类推,每3个数为一个循环组依次循环,
∵2017÷3=672余1,
∴a2017为第673循环组的第一个数,
∴a2017=a1=-$\frac{1}{3}$.
故答案为:-$\frac{1}{3}$.
点评 本题是对数字变化规律的考查,读懂题目信息,理解差倒数的定义并求出3个数为一个循环组依次循环是解题的关键,也是本题的难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.某市区某天的最高气温是8℃,最低气温是零下4℃,则该地这一天的温差是( )
| A. | -10℃ | B. | -8℃ | C. | 8℃ | D. | 12℃ |
7.一种面粉包装袋上的质量标识为“10±0.1”千克,则下列面粉质量合格的是( )
| A. | 9.91千克 | B. | 10.2千克 | C. | 9.89千克 | D. | 10.11千克 |
14.下列各图不是正方体表面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
8.已知$\overrightarrow{a}$、$\overrightarrow{b}$和$\overrightarrow{c}$都是非零向量,在下列选项中,不能判定$\overrightarrow{a}∥\overrightarrow{b}$的是( )
| A. | $\overrightarrow{a}∥\overrightarrow{c}$,$\overrightarrow{b}∥\overrightarrow{c}$ | B. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | C. | $\overrightarrow{a}=2\overrightarrow{b}$ | D. | $\overrightarrow{a}=\frac{1}{2}\overrightarrow{c}$,$\overrightarrow{b}=2\overrightarrow{c}$ |
9.关于x的一元二次方程x2+mx+m=0有两个相等的实数根,则m的值是( )
| A. | 不存在 | B. | 4 | C. | 0 | D. | 0或4 |
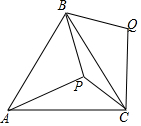 如图,P是等边△ABC内的一点,且PA=5,PB=4,PC=3,将△APB绕点B逆时针旋转,得到△CQB.求:
如图,P是等边△ABC内的一点,且PA=5,PB=4,PC=3,将△APB绕点B逆时针旋转,得到△CQB.求: