题目内容
已知:如图,⊙O与⊙P相交于A、B两点,点P在⊙O上,⊙O的弦AC切⊙P于点A,CP及其延长线交⊙P于D、E,过点 E作EF⊥CE交CB的延长线于F.
E作EF⊥CE交CB的延长线于F.
(1)求证:BC是⊙P的切线;
(2)若CD=2,CB= ,求EF的长;
,求EF的长;
(3)求以BP、EF为根的一元二次方程.
解:(1)∵点P在⊙O上.连接PB,PA,
∵⊙O的弦AC切⊙P于点A,
∴∠CAP=90°.
∵四边形APBC是⊙O的内接四边形,
∴∠PBC=90°,即PB⊥CB.
∵B在⊙P上,
∴CB是⊙P的切线.
(2)∵CB是⊙P的切线,
∴CB2=CD•(CD+DE).
∵CB=2 ,CD=2,
,CD=2,
∴ =2×(2+ED).
=2×(2+ED).
∴DE=2.
∴CE=CD+DE=2+2=4.
∴在⊙P中,PD=PE= ED=1.
ED=1.
∵CP=3,CB=2 ,
,
∴BP=1.
∵EF⊥CE,
∴∠FEC=∠CBP=90°,∠FCE=∠PCB.
∴△FCE∽△PCB.
∴ .
.
∵CB=2 ,CE=4,BP=1,
,CE=4,BP=1,
∴ .
.
∴EF= .
.
(3)∵EF+BP= +1,EF•BP=
+1,EF•BP= ,
,
∴所求以EF,BP为根的一元二次方程是:x2-( +1)x+
+1)x+ =0.
=0.
分析:(1)本题需作辅助线,再根据圆内接四边形对角互补证明∠PBC是直角,从而可以确定CB是⊙P的切线;
(2)根据△FCE∽△PCB,则 ,由于CB是⊙P的切线,所以根据CB2=CD•(CD+DE),可以求得DE的长度,进而求得CE的长度;再求得BP的长度即可,在Rt△CPB中,CP=3,CB=2,则可求得BP的长度;
,由于CB是⊙P的切线,所以根据CB2=CD•(CD+DE),可以求得DE的长度,进而求得CE的长度;再求得BP的长度即可,在Rt△CPB中,CP=3,CB=2,则可求得BP的长度;
(3)由根与系数的关系可知:EF+BP= +1,EF•BP=
+1,EF•BP= 则可确定一元二次方程.
则可确定一元二次方程.
点评:本题考查的是切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.以及根与系数的关系.
∵⊙O的弦AC切⊙P于点A,

∴∠CAP=90°.
∵四边形APBC是⊙O的内接四边形,
∴∠PBC=90°,即PB⊥CB.
∵B在⊙P上,
∴CB是⊙P的切线.
(2)∵CB是⊙P的切线,
∴CB2=CD•(CD+DE).
∵CB=2
 ,CD=2,
,CD=2,∴
 =2×(2+ED).
=2×(2+ED).∴DE=2.
∴CE=CD+DE=2+2=4.
∴在⊙P中,PD=PE=
 ED=1.
ED=1.∵CP=3,CB=2
 ,
,∴BP=1.
∵EF⊥CE,
∴∠FEC=∠CBP=90°,∠FCE=∠PCB.
∴△FCE∽△PCB.
∴
 .
.∵CB=2
 ,CE=4,BP=1,
,CE=4,BP=1,∴
 .
.∴EF=
 .
.(3)∵EF+BP=
 +1,EF•BP=
+1,EF•BP= ,
,∴所求以EF,BP为根的一元二次方程是:x2-(
 +1)x+
+1)x+ =0.
=0.分析:(1)本题需作辅助线,再根据圆内接四边形对角互补证明∠PBC是直角,从而可以确定CB是⊙P的切线;
(2)根据△FCE∽△PCB,则
 ,由于CB是⊙P的切线,所以根据CB2=CD•(CD+DE),可以求得DE的长度,进而求得CE的长度;再求得BP的长度即可,在Rt△CPB中,CP=3,CB=2,则可求得BP的长度;
,由于CB是⊙P的切线,所以根据CB2=CD•(CD+DE),可以求得DE的长度,进而求得CE的长度;再求得BP的长度即可,在Rt△CPB中,CP=3,CB=2,则可求得BP的长度;(3)由根与系数的关系可知:EF+BP=
 +1,EF•BP=
+1,EF•BP= 则可确定一元二次方程.
则可确定一元二次方程.点评:本题考查的是切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.以及根与系数的关系.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.
21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.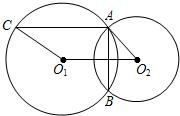 ,⊙O2的半径为
,⊙O2的半径为 14、已知:如图,⊙O1与⊙O2外切于点P,⊙O1的半径为3,且O1O2=8,则⊙O2的半径R=
14、已知:如图,⊙O1与⊙O2外切于点P,⊙O1的半径为3,且O1O2=8,则⊙O2的半径R= (1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D.
(1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D. 已知:如图,⊙O1与⊙O2相交于A,B两点.求证:直线O1O2垂直平分AB.
已知:如图,⊙O1与⊙O2相交于A,B两点.求证:直线O1O2垂直平分AB.