题目内容
2. 抛物线C1:y=a(x+1)(x-3a)(a>0)与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3).
抛物线C1:y=a(x+1)(x-3a)(a>0)与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3).(1)求抛物线C1的解析式及A,B点坐标;
(2)将抛物线C1向上平移3个单位长度,再向左平移n(n>0)个单位长度,得到抛物线C2,若抛物线C2的顶点在△ABC内,求n的取值范围.
分析 (1)根据已知点的坐标代入已知的函数的解析式即可利用待定系数法确定二次函数的解析式;
(2)首先根据平移确定平移后的函数的解析式,然后确定抛物线C2的顶点坐标;结合图形确定n的取值范围即可.
解答 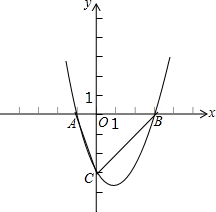 解:(1)∵抛物线C1:y=a(x+1)(x-3a)y轴交于点C(0,-3),
解:(1)∵抛物线C1:y=a(x+1)(x-3a)y轴交于点C(0,-3),
∴-3=a(0+1)(0-3a),
解得a=1(舍去负值).
∴抛物线C1的解析式为:y=(x+1)(x-3).
∴A(-1,0),B(3,0);
(2)∵y=(x+1)(x-3)=(x-1)2-4,
∴该抛物线的解析式为y=(x-1)2-4,则该抛物线的顶点坐标为(1,-4).
将(1)中求得的抛物线向上平移3个单位长度,
再向左平移n(n>0)个单位长度得到新抛物线y=(x-1+n)2-1,
∴平移后抛物线的顶点坐标是(1-n,-1),
∴-$\frac{2}{3}$<1-n<2,
解得-1<n<$\frac{5}{3}$,
∵n>0,
∴0<n<$\frac{5}{3}$.
点评 本题考查了二次函数图象与几何变换,题目中还渗透了数形结合的数学思想,这也是中考中常常出现的重要的数学思想,应加强此类题目的训练.

练习册系列答案
相关题目
13.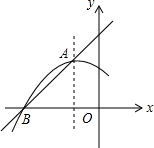 如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点A的坐标为(-1,2),与x轴的一个交点B的坐标为(-3,0),直线y2=mx+n与抛物线交于A、B两点.下列结论:①2a-b=0;②abc<0;③a+b+c=0;④方程ax2+bx+c=5没有实数根;⑤当y1<y2时,x>-1.其中正确的是( )
如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点A的坐标为(-1,2),与x轴的一个交点B的坐标为(-3,0),直线y2=mx+n与抛物线交于A、B两点.下列结论:①2a-b=0;②abc<0;③a+b+c=0;④方程ax2+bx+c=5没有实数根;⑤当y1<y2时,x>-1.其中正确的是( )
 如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点A的坐标为(-1,2),与x轴的一个交点B的坐标为(-3,0),直线y2=mx+n与抛物线交于A、B两点.下列结论:①2a-b=0;②abc<0;③a+b+c=0;④方程ax2+bx+c=5没有实数根;⑤当y1<y2时,x>-1.其中正确的是( )
如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点A的坐标为(-1,2),与x轴的一个交点B的坐标为(-3,0),直线y2=mx+n与抛物线交于A、B两点.下列结论:①2a-b=0;②abc<0;③a+b+c=0;④方程ax2+bx+c=5没有实数根;⑤当y1<y2时,x>-1.其中正确的是( )| A. | ①③④ | B. | ①③④⑤ | C. | ①③⑤ | D. | ②③④⑤ |
17.下列各数中,为无理数的是( )
| A. | tan45° | B. | π0 | C. | $\sqrt{2}$ | D. | -3 |
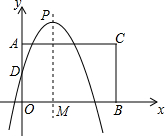 如图,在平面直角坐标系中,点A,B分别是y轴正半轴,x轴正半轴上两动点,OA=2k,OB=2k+3,以AO,BO为邻边构造矩形AOBC,抛物线y=-$\frac{3}{4}$x2+3x+k交y轴于点D,P为顶点,PM⊥x轴于点M.
如图,在平面直角坐标系中,点A,B分别是y轴正半轴,x轴正半轴上两动点,OA=2k,OB=2k+3,以AO,BO为邻边构造矩形AOBC,抛物线y=-$\frac{3}{4}$x2+3x+k交y轴于点D,P为顶点,PM⊥x轴于点M.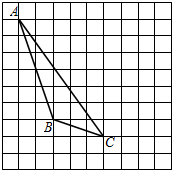 如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′,利用网格点和直尺画图.
如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′,利用网格点和直尺画图. 的图象与一次函数
的图象与一次函数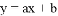 的图象相交于点A(1,4)和点B(n,-2).
的图象相交于点A(1,4)和点B(n,-2).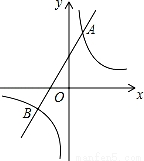
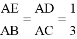 ,则
,则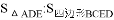 的值为( )
的值为( )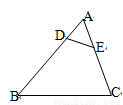
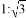 B. 1:3 C. 1:8 D. 1:9
B. 1:3 C. 1:8 D. 1:9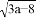 与
与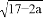 能够合并,那么a的值为______.
能够合并,那么a的值为______.