题目内容
若mx3yp与nxm+1y2的和为0,则m-n+3p= .
考点:合并同类项
专题:
分析:根据题意可知:mx3yp和nxm+1y2为同类项,然后列方程求解.
解答:解:由题意得,mx3yp+nxm+1y2=0,
即
,
解得:
,
则m-n+3p=2+2+2×3=10.
故答案为:10.
即
|
解得:
|
则m-n+3p=2+2+2×3=10.
故答案为:10.
点评:本题考查了合并同类项的知识,解答本题的关键是掌握同类项定义中相同字母的指数相同.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
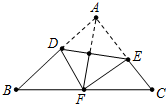 如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中正确的是( )
如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中正确的是( )A、EF∥AB且EF=
| ||
| B、∠BAF=∠CAF | ||
| C、S四边形ADFE=AF•DE | ||
| D、∠BDF+∠FEC=2∠BAC |
 将一张宽度相等的纸条按如图所示的方式折叠,则图中∠1的度数为( )
将一张宽度相等的纸条按如图所示的方式折叠,则图中∠1的度数为( )| A、60° | B、55° |
| C、45° | D、35° |
 如图,若∠1与∠2互补,∠2与∠3互补,则( )
如图,若∠1与∠2互补,∠2与∠3互补,则( )| A、l3∥l4 |
| B、l2∥l5 |
| C、l1∥l3 |
| D、l1∥l2 |

 如图,∠ACF=∠BCF,FG∥AC,HG∥FC.试说明∠FGH=∠BGH.
如图,∠ACF=∠BCF,FG∥AC,HG∥FC.试说明∠FGH=∠BGH.