题目内容
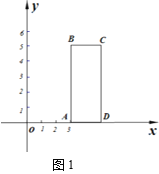
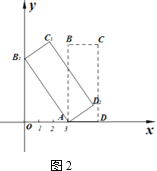
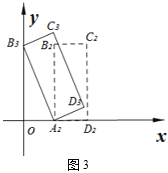
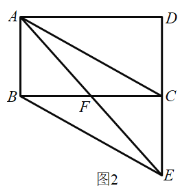
【题目】如图,正方形A0B0C0A1的边长为1,正方形A1B1C1A2的边长为2,正方形A2B2C2A3的边长为4,正方形A3B3C3A4的边长为8……依此规律继续作正方形AnBnnAn+1,且点A0,A1,A2,A3,…,An+1在同一条直线上,连接A0C1交A1B1于点D1,连接A1C2交A2B2于点D2,连接A2C3交A3B3于点D3……记四边形A0B0C0D1的面积为S1,四边形A1B1C1D2的面积为S2,四边形A2B2C2D3的面积为S3……四边形An﹣1Bn﹣1Cn﹣1Dn的面积为Sn,则S2019=_____.
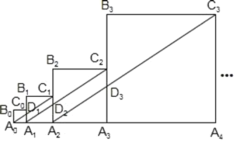
【答案】![]() ×42018
×42018
【解析】
由正方形的性质得出A1D1∥A2C1,则![]() =
=![]() ,得出A1D1=
,得出A1D1=![]() ,同理可得A2D2=
,同理可得A2D2=![]() ,S1=1﹣
,S1=1﹣![]() ×1×
×1×![]() =40﹣
=40﹣![]() ×40,S2=4﹣
×40,S2=4﹣![]() ×4,S3=42﹣
×4,S3=42﹣![]() ×42,…,Sn=4n﹣1﹣
×42,…,Sn=4n﹣1﹣![]() ×4n﹣1=
×4n﹣1=![]() ×4n﹣1,即可得出答案.
×4n﹣1,即可得出答案.
解:∵四边形A0B0C0A1与四边形A1B1C1A2都是正方形,
∴A1D1∥A2C1,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴A1D1=![]() ,
,
同理可得:A2D2=![]() ,
,
∴S1=1﹣![]() ×1×
×1×![]() =40﹣
=40﹣![]() ×40,S2=4﹣
×40,S2=4﹣![]() ×4,S3=42﹣
×4,S3=42﹣![]() ×42,…,Sn=4n﹣1﹣
×42,…,Sn=4n﹣1﹣![]() ×4n﹣1=
×4n﹣1=![]() ×4n﹣1,
×4n﹣1,
∴S2019=![]() ×42018,
×42018,
故答案为:![]() ×42018.
×42018.

练习册系列答案
相关题目
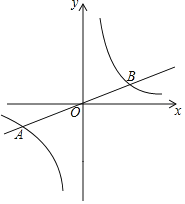
【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() .
.
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
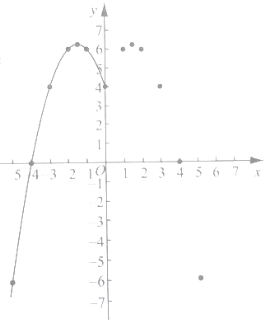
(3)观察函数图象,写出两条函数的性质.
(4)直线![]() 经过
经过![]() ,若关于
,若关于![]() 的方程
的方程![]() 有
有![]() 个不相等的实数根,则
个不相等的实数根,则![]() 的取值范围为 .
的取值范围为 .