题目内容
13.计算:(1)$\sqrt{8}$+$\sqrt{32}$-$\sqrt{2}$
(2)$\sqrt{\frac{1}{3}}$+$\sqrt{27}$×$\sqrt{9}$
(3)$\frac{{2\sqrt{12}+\sqrt{3}}}{{\sqrt{3}}}$+(1-$\sqrt{3}$)0
(4)($\sqrt{5}$-$\sqrt{7}$)($\sqrt{5}$+$\sqrt{7}$)+2.
分析 (1)先化简二次根式,再合并同类二次根式即可;
(2)先化简二次根式,再合并同类二次根式即可;
(3)先化简二次根式,再合并同类二次根式即可;
(4)根据平方差公式进行计算即可.
解答 解:(1)原式=2$\sqrt{2}$+4$\sqrt{2}$-$\sqrt{2}$
=5$\sqrt{2}$;
(2)原式=$\frac{\sqrt{3}}{3}$+9$\sqrt{3}$
=$\frac{28\sqrt{3}}{3}$;
(3)原式=5+1
=6;
(4)原式=5-7+2
=0.
点评 本题考查了二次根式的混合运算,掌握化简二次根式,合并同类项是解题的关键.

练习册系列答案
相关题目
18.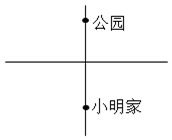 如图,小明周末到公园走到十字路口处,记不清前面哪条路通往公园,那么他能一次选对路的概率是( )
如图,小明周末到公园走到十字路口处,记不清前面哪条路通往公园,那么他能一次选对路的概率是( )
 如图,小明周末到公园走到十字路口处,记不清前面哪条路通往公园,那么他能一次选对路的概率是( )
如图,小明周末到公园走到十字路口处,记不清前面哪条路通往公园,那么他能一次选对路的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | 0 |
2.下列说法,正确的是( )
| A. | -52 与(-5)2相等 | |
| B. | 如果两个数的和为零,那么这两个数一定是一正一负 | |
| C. | -a2表示一个负数 | |
| D. | 两个有理数的差不一定小于被减数 |
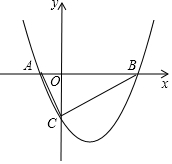 抛物线y=ax2+bx-2与x轴交于点A(-1,0),B(m,0)两点,与y交于点C,且∠ACB=90°,则该抛物线的解析式为y=0.5x2-1.5x-2.
抛物线y=ax2+bx-2与x轴交于点A(-1,0),B(m,0)两点,与y交于点C,且∠ACB=90°,则该抛物线的解析式为y=0.5x2-1.5x-2.




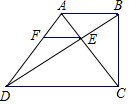 如图,在四边形ABCD中,AB∥CD,∠ABC=90°,CD=2AB,对角线AC与BD相交于点E,EF∥CD交AD于点F.
如图,在四边形ABCD中,AB∥CD,∠ABC=90°,CD=2AB,对角线AC与BD相交于点E,EF∥CD交AD于点F.