题目内容
17.已知关于x的一元二次方程x2-mx-2=0(1)若x=-1是这个方程的一个根,求m的值和方程的另一根;
(2)对于任意的实数m,判断方程的根的情况,并说明理由.
分析 (1)把x=-1代入已知方程,得到关于m的一元一次方程,通过解该方程来求m的值;
(2)由根的判别式的符号来判定原方程的根的情况.
解答 解:(1)将x=-1代入方程x2-mx-2=0,得1+m-2=0,
解得m=1,
解方程x2-x-2=0,解得x1=-1,x2=2;
(2)∵△=m2+8>0,
∴对于任意的实数m,方程有两个不相等的实数根.
点评 本题考查了根的判别式和方程的解的定义.一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;
②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.
上面的结论反过来也成立.

练习册系列答案
相关题目
8.下列计算,正确的是( )
| A. | 6a+a=6a2 | B. | -2a+5b=3ab | C. | 3xy-5xy=-2xy | D. | 4m2n-2mn2=2mn |
9. M,N是两个有理数,由图可知M,N所表示的数分别为( )
M,N是两个有理数,由图可知M,N所表示的数分别为( )
 M,N是两个有理数,由图可知M,N所表示的数分别为( )
M,N是两个有理数,由图可知M,N所表示的数分别为( )| A. | -2.5,2.5 | B. | -1.5,3.5 | C. | 2.5,-1.5 | D. | -1.5,2.5 |
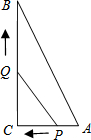 如图,Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,一动点P从点A出发沿边AC向点C以1cm/s的速度运动,另一动点Q同时从点C出发沿CB边向点B以2cm/s的速度运动.问:
如图,Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,一动点P从点A出发沿边AC向点C以1cm/s的速度运动,另一动点Q同时从点C出发沿CB边向点B以2cm/s的速度运动.问: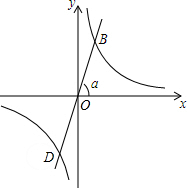 如图,正比例函数的图象与x轴正方向所成角为α,若它与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B,D.
如图,正比例函数的图象与x轴正方向所成角为α,若它与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B,D.