题目内容
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 的中点,在边
的中点,在边![]() 上取点
上取点![]()
![]() ,点
,点![]() 在边
在边![]() 上,且满足
上,且满足![]() ,连接
,连接![]() ,作
,作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,线段
,线段![]() ,
,![]() ,
,![]() 将
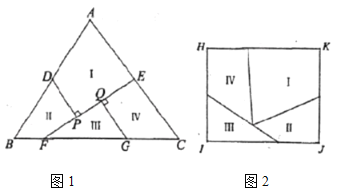
将![]() 分割成I、II、III、IV四个部分,将这四个部分重新拼接可以得到如图2所示的矩形
分割成I、II、III、IV四个部分,将这四个部分重新拼接可以得到如图2所示的矩形![]() ,若
,若![]() ,则图1中
,则图1中![]() 的长为_______.
的长为_______.
【答案】![]()
【解析】
本题可用图一图二等面积性,求解部分边长,利用等腰三角形三线合一以及中位线性质创造三角形全等的条件,通过假设未知数利用三角函数表示未知边长,继而用勾股定理列方程求解本题.
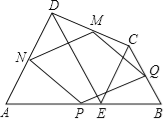
连接DE,DF,作FM⊥AB,AO⊥BC,如下图所示:
∵AB=AC=10,点D,E分别为AB,AC中点,FG=![]() BC,DP⊥EF,GQ⊥EF,BC=12,
BC,DP⊥EF,GQ⊥EF,BC=12,
∴DE∥BC,DE=![]() BC=FG,∠DPE=∠GQF=90°,AO=8,
BC=FG,∠DPE=∠GQF=90°,AO=8,![]() ,
,![]() ,DB=5.
,DB=5.
∴∠DEP=∠GFQ,![]() ,
,
故有△DPE![]() △GQF(AAS),
△GQF(AAS),
∴DP=GQ,FQ=PE.
∵FQ-PQ=PE-PQ,
∴FP=QE.
设HI=4x,IJ=5x,
因为矩形HIJK,故![]() ,
,
∴![]() 且由图形拼接可得:
且由图形拼接可得:![]() ,
,![]() .
.
在△FQG中,![]() ,
,
![]() ,
,
∴在△DPF中,![]() .
.
设BF=y,有![]() ,则
,则![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在△DMF中,![]() ,
,
∴![]() ,
,
解方程求得![]() .
.
故本题答案![]() .
.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】2020蓉漂云招聘活动在4月25日正式启动,共发布了岗位13198个.某网络公司招聘一名高级网络工程师,应聘者小魏参加笔试和面试,成绩(100分制)如表所示:
笔试 | 面试 | |||||||
成绩 | 98 | 评委1 | 评委2 | 评委3 | 评委4 | 评委5 | 评委6 | 评委 7 |
94 | 95 | 92 | 99 | 98 | 97 | 96 | ||
其中规定:面试得分中去掉一个最高分和一个最低分,余下的面试得分的平均值作为应聘者的面试成绩.
(1)请计算小魏的面试成绩;
(2)如果面试成绩与笔试成绩按6:4的比例确定,请计算出小魏的最终成绩.