已知|x|=$\sqrt{5}$.y是3的平方根.且|y-x|=x-y.求x+y的值．题目和参考答案——青夏教育精英家教网—

题目内容

10．已知|x|=$\sqrt{5}$，y是3的平方根，且|y-x|=x-y，求x+y的值．

分析先依据绝对值和平方根的定义确定出x、y的值，然后依据绝对值的性质求得x、y可能的情况，最后进行计算即可．

解答解：由题意得，x=±$\sqrt{5}$，y=±$\sqrt{3}$，
∵|y-x|=x-y，
∴x＞y
∴x=$\sqrt{5}$，y=$\sqrt{3}$或x=$\sqrt{5}$，y=-$\sqrt{3}$．
∴x+y=$\sqrt{5}$+$\sqrt{3}$或x+y=$\sqrt{5}$-$\sqrt{3}$．

点评本题主要考查的是实数的性质、平方根的性质，分类讨论是解题的关键．

练习册系列答案

相关题目

20．

如图，已知A，B，C三点及直线EF，过B点作AB∥EF，过B点作BC∥EF，那么A，B，C三点一定在同一条直线上，依据是过直线外一点，有且只有一条直线与已知直线平行．

1．a，b，c为三个有理数，下列各式可写成a-b+c的是（　　）

18．画△ABC中BC边上的高，下面的画法中，正确的是（　　）

5．探索题：（x-1）（x+1）=x²-1；（x-1）（x²+x+1）=x³-1；（x-1）（x³+x²+x+1）=x⁴-1；（x-1）（x⁴+x³+x²+x+1）=x⁵-1…
根据前面的规律，回答下列问题：
（1）（x-1）（xⁿ+x^n-1+x^n-2+…+x³+x²+x+1）=xⁿ⁺¹-1．
（2）当x=3时，（3-1）（3²⁰¹⁵+3²⁰¹⁴+3²⁰¹³+…+3³+3²+3+1）=3²⁰¹⁶-1．
（3）求：2²⁰¹⁴+2²⁰¹³+2²⁰¹²+…+2³+2²+2+1的值．（请写出解题过程）．

15．已知mx²y^n-1+4x²y⁹=0，（其中x≠0，y≠0）则m+n=（　　）

2．

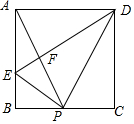如图，在矩形ABCD中，P是BC上一点，E是AB上一点，PD平分∠APC，PE⊥PD，连接DE交AP于F，在以下判断中，不正确的是（　　）

	A．	当P为BC中点，△APD是等边三角形		B．	当△ADE∽△BPE时，P为BC中点
	C．	当AE=2BE时，AP⊥DE		D．	当△APD是等边三角形时，BE+CD=DE

19．

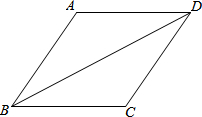如图，四边形ABCD中，∠BCD是钝角，AB=AD，BD平分∠ABC．若CD=3，BD=2$\sqrt{6}$，sin∠DBC=$\frac{\sqrt{3}}{3}$．
（1）求BC的长；
（2）求证：△BCD≌△BAD；
（3）求对角线AC的长．

20．

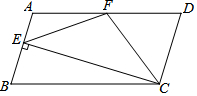如图，在?ABCD中，AD=2AB，F是AD的中点，作CE⊥AB于E，在线段
AB上，连接EF、CF．则下列结论：①∠BCD=2∠DCF；②∠ECF=∠CEF；③S_△BEC=2S_△CEF；④∠DFE=3∠AEF，其中一定正确的是（　　）

试题分类