题目内容
三角形的一边长为a，它的对角为30°，则此三角形的外接圆的半径为________．
a
分析：先根据题意作图（见解答），先求出∠OAD=60°，过O作OD⊥BC，则BD=CD=
，∠1=∠2=30°，在Rt△BOD中，OB=2BD=2×=a，即此三角形的外接圆的半径为a．
解答：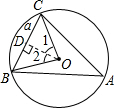
解：如图，∵∠A=30°，
∴∠BOC=60°，∠OBD=∠OCD=
（180°-∠BOC）=（180°-60°）=60°，
过O作OD⊥BC，则
BD=CD=，∠1=∠2=30°，
在Rt△BOD中，∠2=30°，
∴OB=2BD=2×=a，
即此三角形的外接圆的半径为a．
点评：解答此题的关键是根据题意画出图形，利用垂径定理及直角三角形的性质解答．
分析：先根据题意作图（见解答），先求出∠OAD=60°，过O作OD⊥BC，则BD=CD=
，∠1=∠2=30°，在Rt△BOD中，OB=2BD=2×=a，即此三角形的外接圆的半径为a．解答：
解：如图，∵∠A=30°，∴∠BOC=60°，∠OBD=∠OCD=
（180°-∠BOC）=（180°-60°）=60°，过O作OD⊥BC，则
BD=CD=
，∠1=∠2=30°，在Rt△BOD中，∠2=30°，
∴OB=2BD=2×
=a，即此三角形的外接圆的半径为a．
点评：解答此题的关键是根据题意画出图形，利用垂径定理及直角三角形的性质解答．
练习册系列答案
相关题目