题目内容
已知：如图所示，在Rt△ABC中，∠ACB=90°，AC=BC，BD平分∠ABC交AC于D，过点D作DE⊥AB于E，若BC的长为5cm，则△ADE的周长为________．
分析：依题意可证△BDE≌△BDC，则有DE=DC，BE=BC，故DE+DA+AE=DC+DA+AE=CA+AE=BC+AE=BE+AE=AB，再根据勾股定理求AB．
解答：∵BD平分∠ABC交AC于D，过点D作DE⊥AB于E，
∴∠DBE=∠DBC，∠BED=∠C=90°，BD=BD，
∴△BDE≌△BDC，
∴DE=DC，BE=BC，
则DE+DA+AE=DC+DA+AE=CA+AE=BC+AE=BE+AE=AB，
由勾股定理，得AB=
=
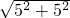=5
cm．故本题答案为：5
cm．点评：本题考查了角平分线性质，勾股定理的运用．关键是根据性质得出相等的线段，再将周长进行转化．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
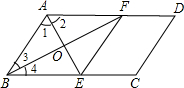阅读下述说明过程，讨论完成下列问题：
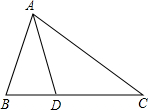已知：如图所示，在△ABC中，AB=AD=DC，∠BAD=26°，求∠B和∠C的度数．
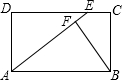已知：如图所示，在矩形ABCD中，E为DC上的一点，BF⊥AE于点F，且BF=BC，求证：AE=AB．
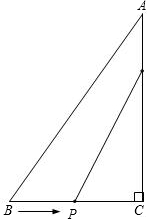同时出发，其中点P以1厘米/秒的速度沿着线段BC向点C运动，点Q以2厘米/秒的速度沿着线段CA向点A运动．
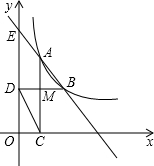点M，连接DC．