Question

（2012•烟台）如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1，0），C（3，0），D（3，4）．以A为顶点的抛物线y=ax²+bx+c过点C．动点P从点A出发，沿线段AB向点B运动．同时动点Q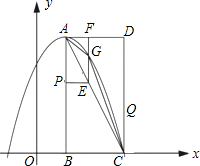从点C出发，沿线段CD向点D运动．点P，Q的运动速度均为每秒1个单位．运动时间为t秒．过点P作PE⊥AB交AC于点E．
（1）直接写出点A的坐标，并求出抛物线的解析式；
（2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？
（3）在动点P，Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C，Q，E，H为顶点的四边形为菱形？请直接写出t的值．

Answer 1

分析：（1）根据矩形的性质可以写出点A得到坐标；由顶点A的坐标可设该抛物线的顶点式方程为y=a（x-1）²+4，然后将点C的坐标代入，即可求得系数a的值（利用待定系数法求抛物线的解析式）；
（2）利用待定系数法求得直线AC的方程y=-2x+6；由图形与坐标变换可以求得点P的坐标（1，4-t），据此可以求得点E的纵坐标，将其代入直线AC方程可以求得点E或点G的横坐标；然后结合抛物线方程、图形与坐标变换可以求得GE=4-

t2

4

、点A到GE的距离为

t

2

，C到GE的距离为2-

t

2

；最后根据三角形的面积公式可以求得
S_△ACG=S_△AEG+S_△CEG=-

1

4

（t-2）²+1，由二次函数的最值可以解得t=2时，S_△ACG的最大值为1；
（3）因为菱形是邻边相等的平行四边形，所以点H在直线EF上．

解答：解：（1）A（1，4）．…（1分）
由题意知，可设抛物线解析式为y=a（x-1）²+4
∵抛物线过点C（3，0），
∴0=a（3-1）²+4，
解得，a=-1，
∴抛物线的解析式为y=-（x-1）²+4，即y=-x²+2x+3．…（2分）

（2）∵A（1，4），C（3，0），
∴可求直线AC的解析式为y=-2x+6．
∵点P（1，4-t）．…（3分）
∴将y=4-t代入y=-2x+6中，解得点E的横坐标为x=1+

t

2

．…（4分）
∴点G的横坐标为1+

t

2

，代入抛物线的解析式中，可求点G的纵坐标为4-

t2

4

．
∴GE=（4-

t2

4

）-（4-t）=t-

t2

4

．…（5分）
又∵点A到GE的距离为

t

2

，C到GE的距离为2-

t

2

，
即S_△ACG=S_△AEG+S_△CEG=

1

2

•EG•

t

2

+

1

2

•EG（2-

t

2

）
=

1

2

•2（t-

t2

4

）=-

1

4

（t-2）²+1．…（7分）
当t=2时，S_△ACG的最大值为1．…（8分）

（3）第一种情况如图1所示，点H在AC的上方，由四边形CQHE是菱形知CQ=CE=t，
根据△APE∽△ABC，知

AP

AB

=

AE

AC

，即

t

4

=

2 5 -t

2 5

，解得t=20-8

5

；
第二种情况如图2所示，点H在AC的下方，由四边形CQHE是菱形知CQ=QE=EH=HC=t，PE=

1

2

t，EM=2-

1

2

t，MQ=4-2t．
则在直角三角形EMQ中，根据勾股定理知EM²+MQ²=EQ²，即（2-

1

2

t）²+（4-2t）²=t²，
解得，t₁=

20

13

，t₂=4（不合题意，舍去）．
综上所述，t=20-8

5

或t=

20

13

．…（12分）
（说明：每值各占（2分），多出的值未舍去，每个扣1分）

点评：本题考查了二次函数的综合题．其中涉及到的知识点有待定系数法求二次函数的解析式，待定系数法求一次函数的解析式以及三角形面积的求法．