题目内容
7.定义运算:a?b=a(1-b).若a,b是方程x2-x+$\frac{1}{4}$m=0(m<0)的两根,则b?b-a?a的值为( )| A. | 0 | B. | 1 | C. | 2 | D. | 与m有关 |
分析 (方法一)由根与系数的关系可找出a+b=1,根据新运算找出b?b-a?a=b(1-b)-a(1-a),将其中的1替换成a+b,即可得出结论.
(方法二)由根与系数的关系可找出a+b=1,根据新运算找出b?b-a?a=(a-b)(a+b-1),代入a+b=1即可得出结论.
(方法三)由一元二次方程的解可得出a2-a=-$\frac{1}{4}$m、b2-b=-$\frac{1}{4}$m,根据新运算找出b?b-a?a=-(b2-b)+(a2-a),代入后即可得出结论.
解答 解:(方法一)∵a,b是方程x2-x+$\frac{1}{4}$m=0(m<0)的两根,
∴a+b=1,
∴b?b-a?a=b(1-b)-a(1-a)=b(a+b-b)-a(a+b-a)=ab-ab=0.
(方法二)∵a,b是方程x2-x+$\frac{1}{4}$m=0(m<0)的两根,
∴a+b=1.
∵b?b-a?a=b(1-b)-a(1-a)=b-b2-a+a2=(a2-b2)+(b-a)=(a+b)(a-b)-(a-b)=(a-b)(a+b-1),a+b=1,
∴b?b-a?a=(a-b)(a+b-1)=0.
(方法三)∵a,b是方程x2-x+$\frac{1}{4}$m=0(m<0)的两根,
∴a2-a=-$\frac{1}{4}$m,b2-b=-$\frac{1}{4}$m,
∴b?b-a?a=b(1-b)-a(1-a)=-(b2-b)+(a2-a)=$\frac{1}{4}$m-$\frac{1}{4}$m=0.
故选A.
点评 本题考查了根与系数的关系,解题的关键是找出a+b=1.本题属于基础题,难度不大,解决该题型题目时,根据根与系数的关系得出两根之积与两根之和是关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
8.下列各数中,3.14159,-$\root{3}{8}$,0.131131113,…,-π,$\sqrt{25}$,-$\frac{1}{7}$,有理数的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.某班学生分组做抛掷瓶盖实验,各组实验结果如下表:
根据表中的信息,估计掷一枚这样的瓶盖,落地后盖面朝上的概率为0.53.(精确到0.01)
| 累计抛掷次数 | 100 | 200 | 300 | 400 | 500 |
| 盖面朝上次数 | 54 | 105 | 158 | 212 | 264 |
| 盖面朝上频率 | 0.5400 | 0.5250 | 0.5267 | 0.5300 | 0.5280 |
 如图,直线l1∥l2,若∠1=130°,∠2=60°,则∠3=70°.
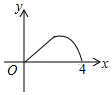
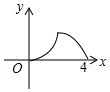
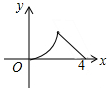
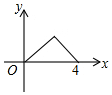
如图,直线l1∥l2,若∠1=130°,∠2=60°,则∠3=70°.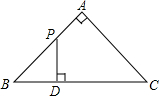 如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )