题目内容
如图①,正方形ABCD的边AB,AD分别在等腰直角△AEF的腰AE,AF上,点C在△AEF内,则有DF=BE(不必证明).将正方形ABCD绕点A逆时针旋转一定角度α(0°<α<90°)后,连结BE,DF.请在图②中用实线补全图形,这时DF=BE还成立吗?请说明理由.
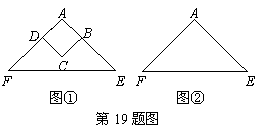
解:补全图形如图所示.
DF=BE还成立,理由是:
∵正方形ABCD和等腰△AEF,
∴AD=AB,AF=AE,∠FAE=∠DAB=90°.
∴∠FAD=∠EAB.
在△ADF和△ABE中,
∴△ADF≌△ABE(SAS).∴DF=BE.



练习册系列答案
相关题目
不等式 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
|
| A. |
| B. |
| C. |
| D. |
|
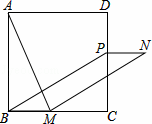
 国结”的图案,按图中规律,第2
国结”的图案,按图中规律,第2 0个图案中,小菱形的个数是多少?
0个图案中,小菱形的个数是多少?
 B.
B. C.
C. D.
D.


 如:将
如:将 转化为分数时,可设
转化为分数时,可设 x,解得x=
x,解得x= 化成分数是 .
化成分数是 . ,以O为圆心,OA长为半径作圆,交AD于M,恰好与BD相切于H,过H
,以O为圆心,OA长为半径作圆,交AD于M,恰好与BD相切于H,过H 作弦HP∥AB,弦HP=3.若点E是CD边上一动点(点E与C,D不重合),过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为G.设CE=x,△EFG与矩形ABCD重叠部分的面积为S.
作弦HP∥AB,弦HP=3.若点E是CD边上一动点(点E与C,D不重合),过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为G.设CE=x,△EFG与矩形ABCD重叠部分的面积为S.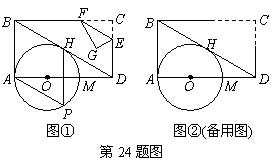




 小虎速度的2倍,求马小虎的速度.
小虎速度的2倍,求马小虎的速度. 的两个实根分别为
的两个实根分别为 、
、 ,那么
,那么 的值为 .
的值为 .